题目内容
表面积为4π的球O与平面角为钝角的二面角的两个半平面相切于A、B两点,三角形OAB的面积S=
,则球心到二面角的棱的距离为______.
| 2 |
| 5 |
由题意,S=4πR2=4π,∴R=1,
根据截面图,PA和PB是球的大圆切线,OP是球心至棱的距离,
∵S△OAB=
R2sin∠AOB=
sin∠AOB=
,
∴sin∠AOB=
,
∴cos∠AOB=
,
∴cos
=
,
∵cos
=
,
∴OP=
.
根据截面图,PA和PB是球的大圆切线,OP是球心至棱的距离,
∵S△OAB=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 5 |
∴sin∠AOB=
| 4 |
| 5 |
∴cos∠AOB=
| 3 |
| 5 |
∴cos
| ∠AOB |
| 2 |
2
| ||
| 5 |
∵cos
| ∠AOB |
| 2 |
| OA |
| OP |
∴OP=
| ||
| 2 |

练习册系列答案
相关题目
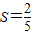 ,则球心到二面角的棱的距离为 .
,则球心到二面角的棱的距离为 .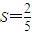 ,则球心到二面角的棱的距离为 .
,则球心到二面角的棱的距离为 .