Question

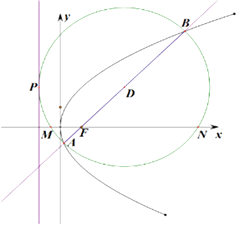
【题目】设过抛物线 的焦点 的直线 交抛物线于点 ，若以 为直径的圆过点 ，且与 轴交于 ， 两点，则 （ ）
A.3
B.2
C.-3
D.-2

Answer 1

【答案】C
【解析】抛物线焦点坐标为F（1，0），准线方程为x=﹣1

设直线MN的方程为x=ty+1，A、B的坐标分别为（ ，y1），（ ，y2）

联立直线和抛物线得到方程：y2﹣4my﹣4=0，

∴y1+y2=4m，y1y2=﹣4，

x1+x2=ty1+1+ty2+1=t（y1+y2）+2=4t2+2， =2t2+1， =2t，

则圆心D（2t2+1，2t），

由抛物线的性质可知：丨AB丨=x1+x2+p=4（t2+1），

由P到圆心的距离d= ，由题意可知：d= 丨AB丨，

解得：t=1，则圆心为（3，2），半径为4，∴圆的方程方程为（x﹣3）2+（y﹣2）2=42，

则当y=0，求得与x轴的交点坐标，假设m＞n，则m=3﹣2 ，n=3+2 ，

∴mn=（3﹣2 ）（3+2 ）=﹣3，

所以答案是：C．

【考点精析】掌握圆的标准方程是解答本题的根本，需要知道圆的标准方程：；圆心为A(a,b),半径为r的圆的方程．