Question

【题目】如图， 是边长为 的正方形， 平面 ， ， ， 与平面 所成角为 ．

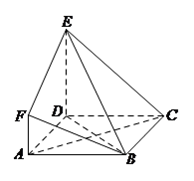
（Ⅰ）求证： 平面 ．
（Ⅱ）求二面角 的余弦值．
（Ⅲ）设点 是线段 上一个动点，试确定点 的位置，使得 平面 ，并证明你的结论．

Answer 1

【答案】解：（Ⅰ）证明：∵ 平面 ， 平面 ，

∴ ，

又∵ 是正方形，

∴ ，

∵ ，

∴ 平面 ．

（Ⅱ）解：∵ ， ， 两两垂直，所以建立如图空间直角坐标系 ，

∵ 与平面 所成角为 ，即 ，

∴ ，

由 ，可知： ， ．

则 ， ， ， ， ，

∴ ， ，

设平面 的法向量为 ，则

，即 ，

令 ，则 ．

因为 平面 ，所以 为平面 的法向量，

∴ ，

所以 ．

因为二面角为锐角，

故二面角 的余弦值为 ．

（Ⅲ）解：依题意得，设 ，

则 ，

∵ 平面 ，

∴ ，即 ，解得： ，

∴点 的坐标为 ，

此时 ，

∴点 是线段 靠近 点的三等分点．

【解析】（1）证明线面垂直的要点就是在平面内找互两条相交直线都与所证直线垂直。
（2）求二面角时，往往建立空间直角坐标系用两个平面的法向量的夹角来求。
（3）要确定点 M 的位置，使得 AM∥平面BEF，可先设点M的坐标，则向量AM与平面的法向量垂直即可。