题目内容
1．过抛物线y2=2px（p＞0）的焦点F的直线l交抛物线于A，B两点，交其准线于点C，若|AF|=6，且|BC|=2|BF|，则此抛物线方程为（ ）| A． | y2=4x | B． | y2=6x | C． | y2=8x | D． | y2=9x |
分析 分别过A、B作准线的垂线，利用抛物线定义将A、B到焦点的距离转化为到准线的距离，结合已知比例关系，即可得p值，进而可得方程．
解答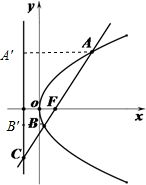 
解：设A，B在准线上的射影分别为A′，B′，则
由于|BC|=2|BB′|，则直线l的斜率为$\sqrt{3}$，
故|AC|=2|AA′|=12，从而|BF|=2，|AB|=8．
故$\frac{p}{|AA′|}=\frac{|CF|}{|CA|}$=$\frac{1}{2}$，即p=3，
从而抛物线的方程为y2=6x．
故选：B．
点评 本题考查抛物线的定义及其应用，抛物线的几何性质，过焦点的弦的弦长关系，转化化归的思想方法，属中档题．
练习册系列答案
阅读快车系列答案
相关题目
6．若f（4x）=x，则f（2）等于（ ）
| A． | 42 | B． | 24 | C． | $\frac{1}{2}$ | D． | 2 |
9．
某县有甲乙丙丁四所高中的五千名学生参加了高三的调研测试，为了解数学学科的成绩情况，现从中随机抽取若干名学生在这次测试中的数学成绩作为样本，（其中甲学校抽取了30人），制成如下频率分布表并得到相应的频率分布直方图：
（1）填写频率分布表．
（2）该次统计中抽取样本的合理方法是什么，甲学校共有多少人参加了调研测试：
（3）从样本在[80，100）的个体中任意抽取2个个体，求至少有一个个体落在[90，100）的概率．
某县有甲乙丙丁四所高中的五千名学生参加了高三的调研测试，为了解数学学科的成绩情况，现从中随机抽取若干名学生在这次测试中的数学成绩作为样本，（其中甲学校抽取了30人），制成如下频率分布表并得到相应的频率分布直方图：| 分组 | 频数 | 频率 |
| [80，90） | 0.025 | |
| [90，100） | 6 | |
| [100，110） | ||
| [110，120） | ||
| [120，130） | ||
| [130，140） | 12 | |
| [140，150） | 0.05 | |
| 合计 |
（2）该次统计中抽取样本的合理方法是什么，甲学校共有多少人参加了调研测试：
（3）从样本在[80，100）的个体中任意抽取2个个体，求至少有一个个体落在[90，100）的概率．
6．
如图，A，B，C，D为⊙O的四等分点，动点P从圆心O出发，沿O-C-D-O路线作匀速运动，设运动时间为t（s）．∠APB=y（单位：度），则下列图象中表示y与t之间函数关系最恰当的是（ ）
如图，A，B，C，D为⊙O的四等分点，动点P从圆心O出发，沿O-C-D-O路线作匀速运动，设运动时间为t（s）．∠APB=y（单位：度），则下列图象中表示y与t之间函数关系最恰当的是（ ）| A． |  | B． |  | C． |  | D． |  |
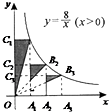如图所示，点A1、A2、A3在x轴上，且OA1=A1A2=A2A3，分别过点A1、A2、A3作y轴的平行线，与反比例函数y=$\frac{8}{x}（{x＞0}）$的图象分别交于点B1、B2、B3，分别过点B1，B2，B3作x轴的平行线，分别与y轴交于点C1，C2，C3，连接OB1，OB2，OB3，那么图中阴影部分的面积之和为$\frac{49}{9}$．
10．已知f（x）=$\left\{\begin{array}{l}{a}^{x}，x＜0\\（a-3）x+4a，x≥0\end{array}\right.$满足对任意x1≠x2，都有[f（x1）-f（x2）]（x1-x2）＜0成立，则a的取值范围是（ ）
| A． | $（{0，\frac{1}{4}}]$ | B． | （0，1） | C． | $[{\frac{1}{4}，1}）$ | D． | （0，3） |