题目内容
已知函数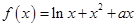 ,
,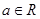 .
.
(1)若函数 在其定义域上为增函数,求
在其定义域上为增函数,求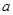 的取值范围;
的取值范围;
(2)当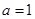 时,函数
时,函数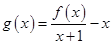 在区间
在区间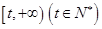 上存在极值,求
上存在极值,求 的最大值.
的最大值.
(参考数值:自然对数的底数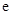 ≈
≈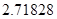 ).
).
(1)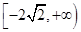 ;(2)
;(2)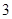 .
.
解析试题分析:(1)解法1是将函数 在其定义域
在其定义域 上为增函数等价转化为不等式
上为增函数等价转化为不等式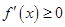 在区间
在区间 上恒成立,利用参数分离法得到不等式
上恒成立,利用参数分离法得到不等式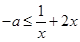 在
在 上恒成立,并利用基本不等式求出
上恒成立,并利用基本不等式求出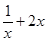 的最小值,从而求出
的最小值,从而求出 的取值范围;解法2是求得导数
的取值范围;解法2是求得导数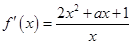 ,将问题等价转化为不等式
,将问题等价转化为不等式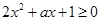 在
在 上恒成立,结合二次函数零点分布的知识求出
上恒成立,结合二次函数零点分布的知识求出 的取值范围;(2)先将
的取值范围;(2)先将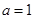 代入函数
代入函数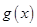 的解析式并求出
的解析式并求出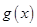 的导数
的导数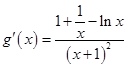 ,构造新函数
,构造新函数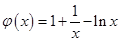 ,利用导数研究函数
,利用导数研究函数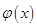 的单调性,结合零点存在定理找出函数
的单调性,结合零点存在定理找出函数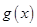 的极值点所存在的区间,结合条件
的极值点所存在的区间,结合条件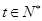 确定
确定 的最大值.
的最大值.
试题解析:(1)解法1:函数 的定义域为
的定义域为 ,
,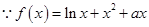 ,
,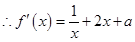 .
.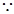 函数
函数 在
在 上单调递增,
上单调递增,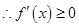 ,即
,即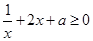 对
对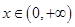 都成立.
都成立.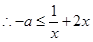 对
对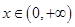 都成立.
都成立.
当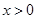 时,
时,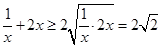 ,当且仅当
,当且仅当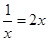 ,即
,即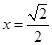 时,取等号.
时,取等号.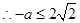 ,即
,即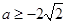 ,
,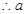 的取值范围为
的取值范围为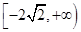 .
.
解法2:函数 的定义域为
的定义域为 ,
,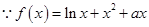 ,
,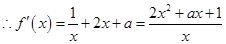 .
.
方程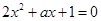 的判别式
的判别式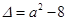 .
.
①当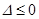 ,即
,即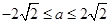 时,
时,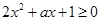 ,
,
此时,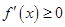 对
对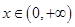 都成立,
都成立,
故函数 在定义域
在定义域 上是增函数.
上是增函数.
②当 ,即
,即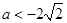 或
或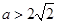 时,要使函数
时,要使函数 在定义域
在定义域 上为增函数,
上为增函数,
只需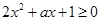 对
对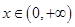 都成立.
都成立.
设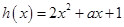 ,则
,则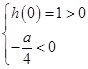 ,得
,得 .
.
故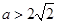 .
.
综合①②得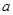 的取值范围为
的取值范围为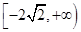 ;
;
(2)当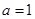 时,
时,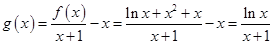 .
.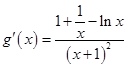 .
. 函数
函数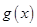 在
在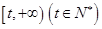 上存在极值,
上存在极值,
∴方程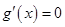 在
在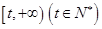

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
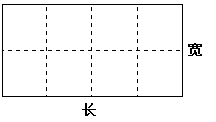
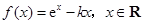
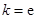 ,试确定函数
,试确定函数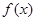 的单调区间;
的单调区间;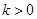 ,且对于任意
,且对于任意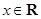 ,
,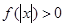 恒成立,试确定实数
恒成立,试确定实数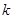 的取值范围;
的取值范围;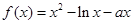 ,
, .
.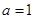 时,求
时,求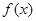 的最小值;
的最小值;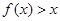 ,求a的取值范围.
,求a的取值范围.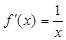 ,
,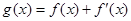 .
.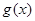 的单调区间和最小值;
的单调区间和最小值;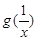 的大小关系;
的大小关系;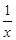 对任意x>0成立?若存在,求出x0的取值范围;若不存在请说明理由.
对任意x>0成立?若存在,求出x0的取值范围;若不存在请说明理由.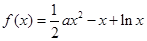 (
(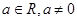 )
) 时,求曲线
时,求曲线 在
在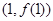 处的切线方程;
处的切线方程; 上函数
上函数 的图象恒在直线
的图象恒在直线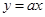 下方,求
下方,求 的取值范围.
的取值范围.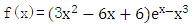
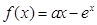
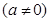 .
.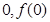 )处的切线方程;
)处的切线方程;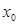 使得
使得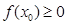 ,求
,求 的取值范围.
的取值范围. .
. 时,求函数
时,求函数 的单调区间;
的单调区间; 上为减函数,求实数
上为减函数,求实数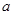 的取值范围;
的取值范围; 时,不等式
时,不等式 恒成立,求实数
恒成立,求实数