题目内容
已知函数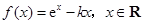
(1)若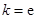 ,试确定函数
,试确定函数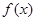 的单调区间;
的单调区间;
(2)若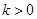 ,且对于任意
,且对于任意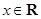 ,
,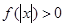 恒成立,试确定实数
恒成立,试确定实数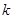 的取值范围;
的取值范围;
(1)详见解析(2)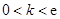 .
.
解析试题分析:(1)求出函数的导数,只要解导数的不等式即可,根据导数与0的关系判断函数的单调性;
(2)函数f(|x|)是偶函数,只要f(x)>0对任意x≥0恒成立即可,等价于f(x)在[0,+∞)的最小值大于零.
试题解析:解:(1)由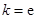 得
得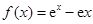 ,所以
,所以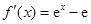 .
.
由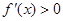 得
得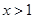 ,故
,故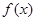 的单调递增区间是
的单调递增区间是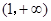 ,
,
由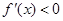 得
得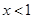 ,故
,故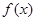 的单调递减区间是
的单调递减区间是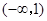 . 4
. 4
(2)由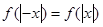 可知
可知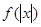 是偶函数.
是偶函数.
于是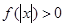 对任意
对任意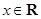 成立等价于
成立等价于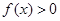 对任意
对任意 成立.
成立.
由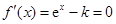 得
得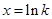 .
.
①当 时,
时,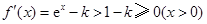 .
.
此时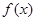 在
在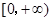 上单调递增.
上单调递增.
故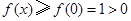 ,符合题意.
,符合题意.
②当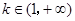 时,
时,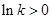 .
.
当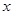 变化时
变化时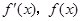 的变化情况如下表:
的变化情况如下表:
由此可得,在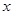
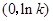
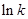
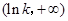
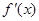
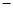

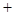
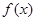
单调递减 极小值 单调递增 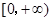 上,
上,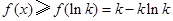 .
.
依题意,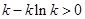 ,又
,又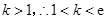 .
.
综合①,②得,实数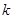 的取值范围是
的取值范围是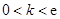 .
.
考点:1.利用导数求闭区间上函数的最值;2.利用导数研究函数的单调性..

练习册系列答案
相关题目
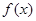 是定义在
是定义在 上的奇函数,当
上的奇函数,当 时,
时,  (其中e是自然界对数的底,
(其中e是自然界对数的底, )
) ,求证:当
,求证:当 时,且
时,且 ,
,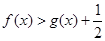 恒成立;
恒成立;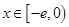 时,
时,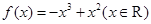 ,
, 满足
满足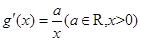 ,且
,且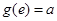 ,
, 为自然对数的底数.
为自然对数的底数.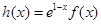 ,求
,求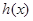 在
在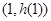 处的切线方程;
处的切线方程;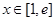 ,使得
,使得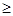
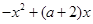 成立,求
成立,求 的取值范围;
的取值范围;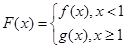 ,
, 为坐标原点,若对于
为坐标原点,若对于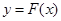 在
在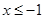 时的图象上的任一点
时的图象上的任一点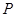 ,在曲线
,在曲线 上总存在一点
上总存在一点 ,使得
,使得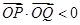 ,且
,且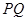 的中点在
的中点在 轴上,求
轴上,求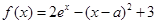 ,
,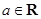 .
.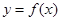 的图象在
的图象在 处的切线与
处的切线与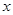 轴平行,求
轴平行,求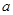 的值;
的值;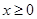 ,
,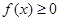 恒成立,求
恒成立,求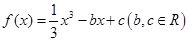 .
.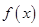 在点
在点 处的切线方程为
处的切线方程为 ,求
,求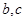 的值;
的值; ,函数
,函数 在区间
在区间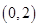 内有唯一零点,求
内有唯一零点,求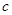 的取值范围;
的取值范围;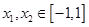 ,均有
,均有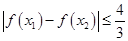 ,求
,求 的取值范围.
的取值范围.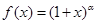 的定义域是
的定义域是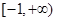 ,其中常数
,其中常数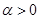 .
.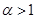 ,求
,求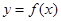 的过原点的切线方程.
的过原点的切线方程.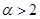 时,求最大实数
时,求最大实数 ,使不等式
,使不等式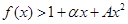 对
对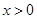 恒成立.
恒成立.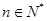 ,有
,有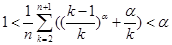 .
.
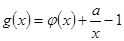 在点
在点 处的切线与直线
处的切线与直线 平行,求
平行,求 的值;
的值; ,
,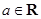 ,且
,且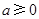 .求函数
.求函数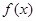 的单调递增区间.
的单调递增区间.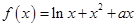 ,
,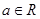 .
. 在其定义域上为增函数,求
在其定义域上为增函数,求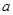 的取值范围;
的取值范围;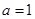 时,函数
时,函数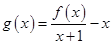 在区间
在区间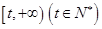 上存在极值,求
上存在极值,求 的最大值.
的最大值.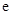 ≈
≈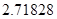 ).
).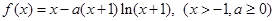 .
. 的单调区间;
的单调区间;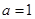 时,若方程
时,若方程 在
在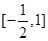 上有两个实数解,求实数
上有两个实数解,求实数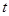 的取值范围;
的取值范围; 时,
时,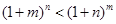 .
.