题目内容
已知点N(1,2),过点N的直线交双曲线x2-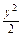 =1于A、B两点,且
=1于A、B两点,且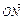 =
=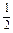 (
(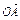 +
+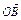 ).
).
(1)求直线AB的方程;
(2)若过N的直线交双曲线于C、D两点,且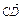 ·
·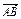 =0,那么A、B、C、D四点是否共圆?为什么?
=0,那么A、B、C、D四点是否共圆?为什么?
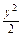 =1于A、B两点,且
=1于A、B两点,且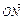 =
=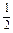 (
(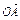 +
+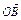 ).
).(1)求直线AB的方程;
(2)若过N的直线交双曲线于C、D两点,且
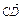 ·
·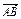 =0,那么A、B、C、D四点是否共圆?为什么?
=0,那么A、B、C、D四点是否共圆?为什么?(1)直线AB的方程为y=x+1(2)A、B、C、D四点共圆
(1)由题意知直线AB的斜率存在.
设直线AB:y=k(x-1)+2,代入x2-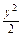 =1
=1
得(2-k2)x2-2k(2-k)x-(2-k)2-2="0. " (*)
令A(x1,y1),B(x2,y2),则x1、x2是方程(*)的两根,
∴2-k2≠0且x1+x2= .
.
∵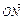 =
=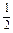 (
(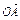 +
+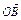 ),∴N是AB的中点,∴
),∴N是AB的中点,∴ =1,
=1,
∴k(2-k)=-k2+2,k=1,
∴直线AB的方程为y=x+1.
(2)将k=1代入方程(*)得x2-2x-3=0,
解得x=-1或x=3,
∴不妨设A(-1,0),B(3,4).
∵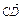 ·
· =0,∴CD垂直平分AB,
=0,∴CD垂直平分AB,
∴CD所在直线方程为y=-(x-1)+2,
即y=3-x,代入双曲线方程整理得x2+6x-11=0,
令C(x3,y3),D(x4,y4)及CD中点M(x0,y0)
则x3+x4=-6,x3·x4=-11,
∴x0= =-3,y0=6,即M(-3,6).
=-3,y0=6,即M(-3,6).
|CD|= |x3-x4|=
|x3-x4|=
 =4
=4 ;
;
|MC|=|MD|=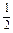 |CD|=2
|CD|=2 ,
,
|MA|=|MB|=2 ,
,
即A、B、C、D到M距离相等,∴A、B、C、D四点共圆.
设直线AB:y=k(x-1)+2,代入x2-
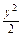 =1
=1得(2-k2)x2-2k(2-k)x-(2-k)2-2="0. " (*)
令A(x1,y1),B(x2,y2),则x1、x2是方程(*)的两根,
∴2-k2≠0且x1+x2=
 .
.∵
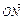 =
=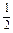 (
(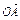 +
+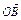 ),∴N是AB的中点,∴
),∴N是AB的中点,∴ =1,
=1,∴k(2-k)=-k2+2,k=1,
∴直线AB的方程为y=x+1.
(2)将k=1代入方程(*)得x2-2x-3=0,
解得x=-1或x=3,
∴不妨设A(-1,0),B(3,4).
∵
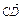 ·
· =0,∴CD垂直平分AB,
=0,∴CD垂直平分AB,∴CD所在直线方程为y=-(x-1)+2,
即y=3-x,代入双曲线方程整理得x2+6x-11=0,
令C(x3,y3),D(x4,y4)及CD中点M(x0,y0)
则x3+x4=-6,x3·x4=-11,
∴x0=
 =-3,y0=6,即M(-3,6).
=-3,y0=6,即M(-3,6).|CD|=
 |x3-x4|=
|x3-x4|=
 =4
=4 ;
;|MC|=|MD|=
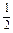 |CD|=2
|CD|=2 ,
,|MA|=|MB|=2
 ,
,即A、B、C、D到M距离相等,∴A、B、C、D四点共圆.

练习册系列答案
相关题目
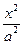 -
-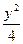 =1过点(-3
=1过点(-3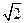 ,2),则该双曲线的焦距为__________.
,2),则该双曲线的焦距为__________. ,并且与直线y=
,并且与直线y=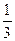 (x-4)相交所得线段的中点的横坐标为-
(x-4)相交所得线段的中点的横坐标为-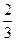 ,求这个双曲线的方程.
,求这个双曲线的方程. 、F
、F 为双曲线
为双曲线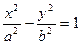 (a>0,b>0)的焦点,过F
(a>0,b>0)的焦点,过F ,求双曲线的渐近线方程。
,求双曲线的渐近线方程。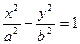 的左焦点为
的左焦点为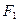 ,顶点为
,顶点为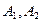 ,
,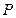 是该双曲线右支上任意一点,则分别以线段
是该双曲线右支上任意一点,则分别以线段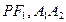 为直径的两圆一定( )
为直径的两圆一定( )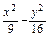 =1有共同的渐近线,且过点(-3,2
=1有共同的渐近线,且过点(-3,2 );求双曲线的标准方程.
);求双曲线的标准方程. 取何实数,直线
取何实数,直线 与双曲线
与双曲线 总有公共点,试求实数
总有公共点,试求实数 的取值范围.
的取值范围.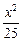 +
+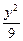 =1的焦点为焦点,离心率e=2的双曲线方程是
=1的焦点为焦点,离心率e=2的双曲线方程是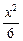 -
-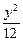 ="1"
="1"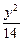 =1
=1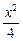 -
-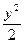 =1上的两点,点N(1,2)是线段AB的中点.
=1上的两点,点N(1,2)是线段AB的中点.