题目内容
已知双曲线的中心在原点,对称轴为坐标轴,焦点在x轴上,两准线间的距离为 ,并且与直线y=
,并且与直线y=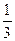 (x-4)相交所得线段的中点的横坐标为-
(x-4)相交所得线段的中点的横坐标为-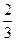 ,求这个双曲线的方程.
,求这个双曲线的方程.
 ,并且与直线y=
,并且与直线y=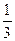 (x-4)相交所得线段的中点的横坐标为-
(x-4)相交所得线段的中点的横坐标为-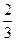 ,求这个双曲线的方程.
,求这个双曲线的方程.双曲线方程为 -
- =1.
=1.
 -
- =1.
=1.设双曲线的方程为 =1(a>0,b>0),直线与双曲线两交点为A(x1,y1)、B(x2,y2).由题意知
=1(a>0,b>0),直线与双曲线两交点为A(x1,y1)、B(x2,y2).由题意知 =
= ,即
,即 =
= .
.
由 得(9b2-a2)x2+8a2x-16a2-9a2b2=0.
得(9b2-a2)x2+8a2x-16a2-9a2b2=0.
∵9b2-a2≠0,由韦达定理得x1+x2= ,即
,即 =-
=-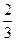 .∴7a2=9b2.
.∴7a2=9b2.
解 得
得 ∴所求双曲线方程为
∴所求双曲线方程为 -
- =1.
=1.
 =1(a>0,b>0),直线与双曲线两交点为A(x1,y1)、B(x2,y2).由题意知
=1(a>0,b>0),直线与双曲线两交点为A(x1,y1)、B(x2,y2).由题意知 =
= ,即
,即 =
= .
.由
 得(9b2-a2)x2+8a2x-16a2-9a2b2=0.
得(9b2-a2)x2+8a2x-16a2-9a2b2=0.∵9b2-a2≠0,由韦达定理得x1+x2=
 ,即
,即 =-
=-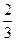 .∴7a2=9b2.
.∴7a2=9b2.解
 得
得 ∴所求双曲线方程为
∴所求双曲线方程为 -
- =1.
=1.
练习册系列答案
相关题目
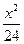 -
-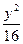 =1,P为双曲线上一点,F1、F2是双曲线的两个焦点,并且∠F1PF2=60°,求△F1PF2的面积.
=1,P为双曲线上一点,F1、F2是双曲线的两个焦点,并且∠F1PF2=60°,求△F1PF2的面积.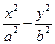 =1(a>0,b>0)的右焦点为F,右准线与一条渐近线交于点A,△OAF的面积为
=1(a>0,b>0)的右焦点为F,右准线与一条渐近线交于点A,△OAF的面积为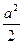 (O为原点),则两条渐近线的夹角为( )
(O为原点),则两条渐近线的夹角为( )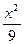 -
-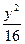 =1只有一个公共点的直线共有______________条.
=1只有一个公共点的直线共有______________条.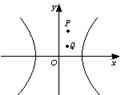
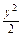 =1于A、B两点,且
=1于A、B两点,且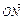 =
=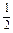 (
(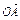 +
+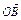 ).
).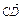 ·
·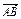 =0,那么A、B、C、D四点是否共圆?为什么?
=0,那么A、B、C、D四点是否共圆?为什么?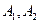 ,垂直于双曲线实轴的直线与双曲线交于
,垂直于双曲线实轴的直线与双曲线交于 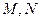 两点,则
两点,则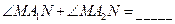
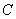 的方程为
的方程为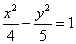 ,若直线
,若直线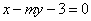 截双曲线的一支所得弦长为5
截双曲线的一支所得弦长为5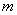 的值;
的值;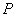 的直线与双曲线的两条渐近线分别交于
的直线与双曲线的两条渐近线分别交于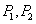 ,且点
,且点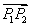 所成的比为
所成的比为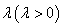 。当
。当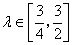 时,求
时,求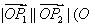 为坐标原点)的最大值和最小值
为坐标原点)的最大值和最小值