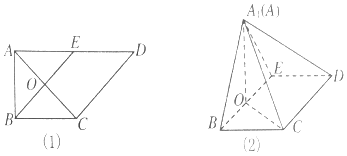
题目内容
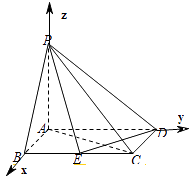
【题目】如图四棱锥P﹣ABCD底面是矩形,PA⊥平面ABCD,PA=AB=1, ![]() ,E是BC上的点,
,E是BC上的点, 
(1)试确定E点的位置使平面PED⊥平面PAC,并证明你的结论;
(2)在条件(1)下,求二面角B﹣PE﹣D的余弦值.
【答案】
(1)证明:以A为原点,AB为x轴,AD为y轴,AP为z轴,建立空间直角坐标系,
∵PA⊥平面ABCD,∴PA⊥DE,
若平面PED⊥平面PAC,
则需要ED⊥平面PAC,
即ED⊥AC即可.
∵PA=AB=1, ![]() ,
,
∴P(0,0,1),D(0, ![]() ,0),B(1,0,0),
,0),B(1,0,0),
C(1, ![]() ,0),
,0),
设BE=a,则E(1,a,0),
则 ![]() =(1,
=(1, ![]() ,0),
,0), ![]() =(﹣1,
=(﹣1, ![]() ﹣a,0),
﹣a,0),
由 ![]()
![]() =(1,
=(1, ![]() ,0)(﹣1,
,0)(﹣1, ![]() ﹣a,0)=0,
﹣a,0)=0,
得﹣1+ ![]() (
( ![]() ﹣a)=0,得a=
﹣a)=0,得a= ![]() ,即E是BC的中点.
,即E是BC的中点.
(2)解:在条件(1)下,即E是BC的中点,则E(1, ![]() ,0),
,0),
则 ![]() =(1,
=(1, ![]() ,﹣1),
,﹣1), ![]() =(0,
=(0, ![]() ,0),
,0), ![]() =(﹣1,
=(﹣1, ![]() ,0),
,0),
设平面BPE的法向量 ![]() =(x,y,z),平面PED的法向量
=(x,y,z),平面PED的法向量 ![]() =(x,y,z),
=(x,y,z),
则由 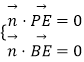 得
得 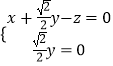 ,即
,即 ![]() ,令x=1,则z=1,即
,令x=1,则z=1,即 ![]() =(1,0,1),
=(1,0,1),
则由 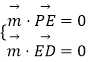 得
得 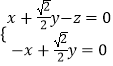 ,令y=
,令y= ![]() ,则x=1,z=2即
,则x=1,z=2即 ![]() =(1,
=(1, ![]() ,2),
,2),
则cos< ![]() ,
, ![]() >|=
>|= ![]() =
= ![]() =
= ![]() =
= ![]() ,
,
∵二面角B﹣PE﹣D是钝二面角,
∴二面角B﹣PE﹣D的余弦值为﹣ ![]() .
.
【解析】(1)以A为原点,AB为x轴,AD为y轴,AP为z轴,建立空间直角坐标系,利用向量法能证明ED⊥AC即可.(2)求出平面的法向量利用向量法即可求二面角B﹣PE﹣D的余弦值.
【考点精析】通过灵活运用平面与平面垂直的性质,掌握两个平面垂直,则一个平面内垂直于交线的直线与另一个平面垂直即可以解答此题.

 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案