��Ŀ����
1�����������R�ϵĺ���f��x�����������x��R������f��-x����-f��x������Ƹú����ǡ��º����������� �ֱ��ж����к�������y=2x����y=2x+1�� ��y=x2-2x-3���Ƿ�Ϊ���º���������ֱ��д�����ۣ�
���� ������f��x��=sinx+cosx+a�ǡ��º���������ʵ��a��ȡֵ��Χ��
���� ��֪f��x��=$\left\{\begin{array}{l}{{x}^{2}+1��x��A}\\{x��x��B}\end{array}\right.$�ǡ��º�����������R�ϵ��������������п��ܵļ���A��B��
���� �����ݡ��º������Ķ����ж����١����ǡ��� ���������۲��ǡ��º�������
���������⣬�������x��R��f��-x��+f��x����0����f��-x��+f��x��=2cosx+2a
�����⣬�������x��R��2cosx+2a��0����a��-cosx���ɵ�ʵ��a��ȡֵ��Χ
����1���������x��0
�֣�a����x��A��-x��A����b����x��B��-x��B����֤
��2���������x0��0��ʹ��x0��A������x0��$\frac{{x}_{0}}{2}$����f��x0����f��$\frac{{x}_{0}}{2}$����
��a����$\frac{{x}_{0}}{2}��A$����f��$\frac{{x}_{0}}{2}$��=$\frac{{{x}_{0}}^{2}}{4}+1��{{x}_{0}}^{2}+1=f��{x}_{0}��$��ì�ܣ�
��b����$\frac{{x}_{0}}{2}��B$����f��$\frac{{x}_{0}}{2}$��=$\frac{{x}_{0}}{2}��0��{{x}_{0}}^{2}+1=f��{x}_{0}��$��ì�ܣ�
��3������0��B����f��-0��=-f��0��=0��ì�ܣ���0��A����A=[0��+�ޣ���B=��-�ޣ�0����
��� �⣺���١����ǡ��� ���������۲��ǡ��º�����������3�֣�
���������⣬�������x��R��f��-x����-f��x������f��-x��+f��x����0����
��Ϊf��x��=sinx+cosx+a������f��-x��=-sinx+cosx+a��
��f��-x��+f��x��=2cosx+2a
�����⣬�������x��R��2cosx+2a��0����a��-cosx������6�֣�
��ʵ��a��ȡֵ��ΧΪ��-�ޣ�-1���ȣ�1��+�ޣ�������8�֣�
����1���������x��0
��a����x��A��-x��A����-x��x��f��-x��=f��x��������y=f��x����R�ϵ�������ì�ܣ����ᣩ��
��b����x��B��-x��B����f-��x��=-x=-f��x��������y=f��x���ǡ��º�����ì�ܣ����ᣩ��
��ʱ����y=f��x���Ķ�����ΪR���ʶ������x��0��x��-xǡ��һ������A����һ������B��
��2���������x0��0��ʹ��x0��A������x0��$\frac{{x}_{0}}{2}$����f��x0����f��$\frac{{x}_{0}}{2}$����
��a����$\frac{{x}_{0}}{2}��A$����f��$\frac{{x}_{0}}{2}$��=$\frac{{{x}_{0}}^{2}}{4}+1��{{x}_{0}}^{2}+1=f��{x}_{0}��$��ì�ܣ�
��b����$\frac{{x}_{0}}{2}��B$����f��$\frac{{x}_{0}}{2}$��=$\frac{{x}_{0}}{2}��0��{{x}_{0}}^{2}+1=f��{x}_{0}��$��ì�ܣ�
���ϣ��������x��0��x∉A����x��B������-�ޣ�0��⊆B����0��+�ޣ�⊆A��
��3������0��B����f��-0��=-f��0��=0��ì�ܣ���0��A
��A=[0��+�ޣ���B=��-�ޣ�0����
������A=[0��+�ޣ���B=��-�ޣ�0������������ ����13�֣�
���� ���⿼�����¶��庯����Ū�嶨�庬���ǹؼ����������DZ���Ļ����������������⣮

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�| A�� | 5 | B�� | $\frac{11}{5}$ | C�� | $\frac{9}{5}$ | D�� | $\frac{7}{5}$ |
| A�� | $\frac{1}{2}$ | B�� | $\frac{1}{3}$ | C�� | $\frac{1}{4}$ | D�� | $\frac{1}{6}$ |
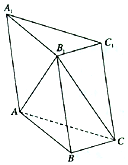 ��ͼ��ʾ����֪������ABC-A1B1C1�У�A1C1=B1C1��A1A=A1B1����AA1B1=60�㣮
��ͼ��ʾ����֪������ABC-A1B1C1�У�A1C1=B1C1��A1A=A1B1����AA1B1=60�㣮 ijУ�����Ŀư�150�������ڡ�ѧ�����ʽ���50���ܡ���������У��ɼ�ȫ������6����11��֮�䣮�ֽ����Խ���ֳ����飺��һ��[6��7]���ڶ��飨7��8]�����������飨10��11]����ͼ�ǰ��������鷽���õ���Ƶ�ʷֲ�ֱ��ͼ�������ұ�����������50���ܳɼ�С�ڻ����7���϶�Ϊ���㣬����֪�����鹲48�ˣ����У�Ŀư���������β����гɼ������������9��
ijУ�����Ŀư�150�������ڡ�ѧ�����ʽ���50���ܡ���������У��ɼ�ȫ������6����11��֮�䣮�ֽ����Խ���ֳ����飺��һ��[6��7]���ڶ��飨7��8]�����������飨10��11]����ͼ�ǰ��������鷽���õ���Ƶ�ʷֲ�ֱ��ͼ�������ұ�����������50���ܳɼ�С�ڻ����7���϶�Ϊ���㣬����֪�����鹲48�ˣ����У�Ŀư���������β����гɼ������������9��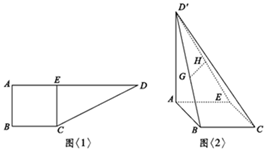 ��ͼ��1������ֱ������ABCD�У�AD��BC����ABC=90�㣬AB=BC=2��AD=6��CE��AD��E�㣬�ѡ�DEC��CE�۵�D��EC��λ�ã�ʹD��A=2$\sqrt{3}$����ͼ��2������G��H�ֱ�ΪD��B��D��E���е㣮
��ͼ��1������ֱ������ABCD�У�AD��BC����ABC=90�㣬AB=BC=2��AD=6��CE��AD��E�㣬�ѡ�DEC��CE�۵�D��EC��λ�ã�ʹD��A=2$\sqrt{3}$����ͼ��2������G��H�ֱ�ΪD��B��D��E���е㣮