题目内容
【题目】已知椭圆
的左、右焦点分别为
，
，离心率为
，过作直线
与椭圆
交于
，
两点，
的周长为8．
（1）求椭圆的标准方程；
（2）问：的内切圆面积是否有最大值？若有，试求出最大值；若没有，说明理由．
【答案】（1）
；（2）
【解析】
（1）由离心率得
，再利用
的周长为8得
，从而得到
的值，进而得到椭圆的方程；
（2）将的内切圆面积的最大值转化为求
的值最大，设
，
，直线
，从而将面积表示成关于
的函数，再利用换元法研究函数的最值.
（1）
离心率为
，
，
的周长为8，
，得，
，
，
因此，椭圆
的标准方程为．
（2）设的内切圆半径为
，
，
又
，
，
要使的内切圆面积最大，只需的值最大．
设，，直线，
联立
消去
得：
，
易得
，且
，
，
所以
，
设
，则
，
设
，
，所以
在
上单调递增，
所以当
，即
时，的最大值为3，
此时
，所以的内切圆面积最大为．
新题型全程检测期末冲刺100分系列答案
【题目】最近，纪录片《美国工厂》引起中美观众热议，大家都认识到，大力发展制造业，是国家强盛的基础，而产业工人的年龄老化成为阻碍美国制造业发展的障碍，中国应未雨绸缪.某工厂有35周岁以上(含35周岁)工人300名，35周岁以下工人200名，为研究工人的日平均生产量是否与年龄有关.现采用分层抽样的方法，从中抽取了100名工人，先统计了他们某月的日平均生产件数，然后按工人年龄在“35周岁以上(含35周岁)”和“35周岁以下”分为两组，在将两组工人的日平均生产件数分成5组:
分别加以统计，得到如图所示的频率分布直方图.
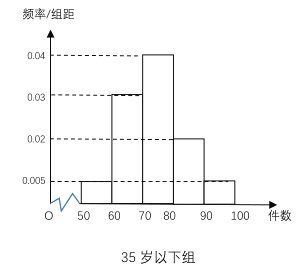
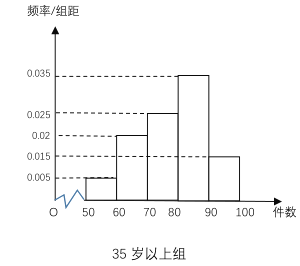
（1）从样本中日平均生产件数不足60件的工人中随机抽取2人，求至少抽到一名“35周岁以下组”工人的概率.
（2）规定日平均生产件数不少于80件者为“生产能手”，请你根据已知条件完成
的列联表，并判断是否有95%的把握认为“生产能手与工人所在的年龄组有关”?
生产能手 | 非生产能手 | 合计 | |
35岁以下 | |||
35岁以上 | |||
合计 |
附表: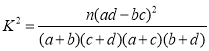
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
