题目内容
已知函数f(x)=lnx+ax2-3x.
(Ⅰ)若f′(2)=1.5,求函数f(x)的极值点.
(Ⅱ)若函数f(x)在[0.5,2]上是减函数,求a的取值范围.
(Ⅰ)若f′(2)=1.5,求函数f(x)的极值点.
(Ⅱ)若函数f(x)在[0.5,2]上是减函数,求a的取值范围.
考点:利用导数研究函数的单调性,利用导数研究函数的极值
专题:导数的综合应用
分析:(Ⅰ)求函数f(x)的极值点,实质是判断函数的单调性,注意函数的定义域,利用导数问题得以解决.
(2)求参数的取值范围,要进行分类讨论,不重不漏的原则.
(2)求参数的取值范围,要进行分类讨论,不重不漏的原则.
解答:
解:(I)∵f(x)=lnx+ax2-3x,(x>0)
∴f′(x)=
+2ax -3,
∴f′(2)=
+4a-3,
又f′(2)=1.5,
∴a=1,
∴f(x)=lnx+x2-3x,
∴f′(x)=
+2x -3=
,
令f′(x)=0,解得,x=1,或x=
,
当f′(x)>0时,即x∈(1,+∞)或(0,
)时,函数f(x)单调递增;
当f′(x)<0时x∈(
,1)函数f(x)单调递减.
∴函函数f(x)的极值点是:x=1,或x=
;
(II)原函数的定义域为(0,+∞),
∴f′(x)=
.
∵函数f(x)在[0.5,2]上是减函数.
∴f′(x)≤0在[0.5,2]恒成立.
①当a>0时,设g(x)=2ax2-3x+1,(x∈[0.5,2])
由题意得:对称轴x=
,
∴
≤
a≤2⇒
≤a≤
时,满足g(x)≤0.
②当a<0时,只需要
a≤
即可,也就是说a≤
,
∴a<0时满足g(x)≤0.
③a=0时,函数g(x)=-3x+1单调递减符合题意.
综上所述:a的取值范围为(-∞,0]∪[
,
].
∴f′(x)=
| 1 |
| x |
∴f′(2)=
| 1 |
| 2 |
又f′(2)=1.5,
∴a=1,
∴f(x)=lnx+x2-3x,
∴f′(x)=
| 1 |
| x |
| 2x2-3x+1 |
| x |
令f′(x)=0,解得,x=1,或x=
| 1 |
| 2 |
当f′(x)>0时,即x∈(1,+∞)或(0,
| 1 |
| 2 |
当f′(x)<0时x∈(
| 1 |
| 2 |
∴函函数f(x)的极值点是:x=1,或x=
| 1 |
| 2 |
(II)原函数的定义域为(0,+∞),
∴f′(x)=
| 2ax2-3x+1 |
| x |
∵函数f(x)在[0.5,2]上是减函数.
∴f′(x)≤0在[0.5,2]恒成立.
①当a>0时,设g(x)=2ax2-3x+1,(x∈[0.5,2])
由题意得:对称轴x=
| 3 |
| 4a |
∴
| 1 |
| 2 |
| 3 |
| 4 |
| 2 |
| 3 |
| 8 |
| 3 |
②当a<0时,只需要
| 3 |
| 4 |
| 1 |
| 2 |
| 2 |
| 3 |
∴a<0时满足g(x)≤0.
③a=0时,函数g(x)=-3x+1单调递减符合题意.
综上所述:a的取值范围为(-∞,0]∪[
| 2 |
| 3 |
| 8 |
| 3 |
点评:本题是导数与函数的单调性的关系,再某个区间上有增函数又有减函数才有极值点,求参数的范围,利用分类讨论的思想,不重不漏.

练习册系列答案
相关题目
设集合M={y|y=cos2x-sin2x|,x∈R},N={x||
|<1,i为虚数单位,x∈R},则M∩N为( )
| 2x | ||
1-
|
| A、(0,1) |
| B、(0,1] |
| C、[0,1) |
| D、[0,1] |
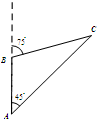 一只艘船以均匀的速度由A点向正北方向航行,如图,开始航行时,从A点观测灯塔C的方位角(从正北方向顺时针转到目标方向的水平角)为45°,行驶60海里后,船在B点观测灯塔C的方位角为75°,则A到C的距离是
一只艘船以均匀的速度由A点向正北方向航行,如图,开始航行时,从A点观测灯塔C的方位角(从正北方向顺时针转到目标方向的水平角)为45°,行驶60海里后,船在B点观测灯塔C的方位角为75°,则A到C的距离是