题目内容
已知{an}满足a1=3，an+1=2an+1，求这个数列的通项公式an．
解：由题意an+1=2an+1可以得到an+1+1=2an+1+1=2（an+1）
所以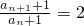
，所以数列{an+1}是以a1+1=4为首项，以2为公比的等比数列．
则有
，
所以
分析：根据数列递推式，变形可得数列{an+1}是以4为首项，以2为公比的等比数列，由此可得结论．
点评：本题考查数列递推式，考查等比数列的判定，考查学生的计算能力，属于基础题．
所以
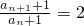，所以数列{an+1}是以a1+1=4为首项，以2为公比的等比数列．则有
，所以
分析：根据数列递推式，变形可得数列{an+1}是以4为首项，以2为公比的等比数列，由此可得结论．
点评：本题考查数列递推式，考查等比数列的判定，考查学生的计算能力，属于基础题．
练习册系列答案
轻松暑假总复习系列答案
相关题目
已知{an}满足a1=a2=1，
-
=1，则a6-a5的值为（ ）
| an+2 |
| an+1 |
| an+1 |
| an |
| A、0 | B、18 | C、96 | D、600 |