题目内容
设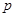 :“
:“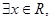
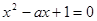 ”,
”,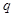 :“函数
:“函数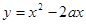
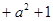 在
在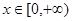 上的值域为
上的值域为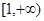 ”,若“
”,若“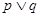 ”是假命题,求实数a的取值范围.
”是假命题,求实数a的取值范围.
【答案】
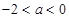 .
.
【解析】
试题分析:“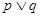 ”是假命题,说明命题
”是假命题,说明命题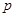 和命题
和命题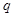 都是假命题,可以求出命题
都是假命题,可以求出命题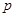 和命题
和命题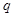 为真时的
为真时的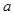 的取值范围,再求它们在实数集
的取值范围,再求它们在实数集 上的补集的并集即可. 命题
上的补集的并集即可. 命题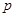 :“
:“
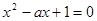 ”,表示方程
”,表示方程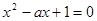 有实数解,命题
有实数解,命题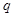 :“函数
:“函数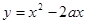
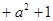 在
在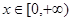 上的值域为
上的值域为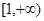 ”,表示
”,表示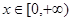 时,函数
时,函数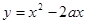
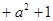 的最小值是1.
的最小值是1.
试题解析:由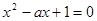 有实根,得
有实根,得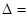
 因此命题p为真命题的范围是
因此命题p为真命题的范围是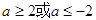 3分
3分
由函数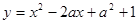 在x
在x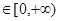 的值域为
的值域为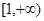 ,得
,得
因此命题q为真命题的范围是 6分
6分
根据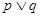 为假命题知:p,q均是假命题,p为假命题对应的范围是
为假命题知:p,q均是假命题,p为假命题对应的范围是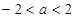 ,q为假命题对应的范围是
,q为假命题对应的范围是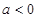 10分
10分
这样得到二者均为假命题的范围就是
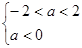
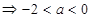 12分
12分
考点:逻辑连接词,一元二次函数在给定区间上的最值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
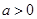 ,且
,且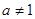 ,则“函数
,则“函数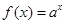 ”在R上是增函数”是“函数
”在R上是增函数”是“函数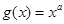 ”在R上是增函数”的( )
”在R上是增函数”的( )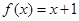 ,设
,设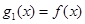 ,
,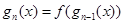
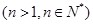 .
.
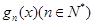 的表达式;此时若设
的表达式;此时若设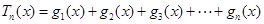 ,且关于
,且关于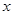 的函数
的函数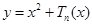
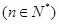 在区间
在区间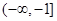 上的最小值为
上的最小值为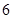 ,则求
,则求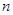 的值;
的值; 为等比数列,数列
为等比数列,数列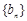 满足
满足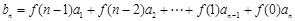 ,
,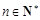 ,若
,若
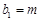 ,
,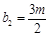 ,其中
,其中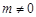 ,则
,则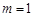 时,求
时,求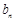 ;
;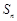 为数列
为数列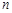 项和,若对于任意的正整数
项和,若对于任意的正整数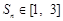 ,求实数
,求实数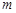 的取值范围.
的取值范围.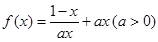 .
.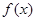 在
在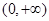 的单调性;
的单调性;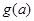 为
为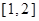 上的最大值,写出
上的最大值,写出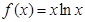 ,
, ,其中
,其中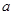 为实数.
为实数. 为常数,求函数
为常数,求函数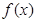 在区间
在区间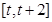 上的最小值;
上的最小值;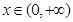 ,不等式
,不等式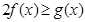 恒成立,求实数
恒成立,求实数 ,设
,设 ,
,
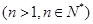 .
. ,
, 的表达式,并直接写出
的表达式,并直接写出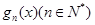 的表达式;
的表达式; ,
, 的函数
的函数
 在区间
在区间 上的最小值为
上的最小值为 ,求
,求 的值.
的值.