题目内容
已知函数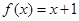 ,设
,设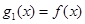 ,
,
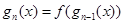
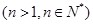 .
.
(1)猜测并直接写出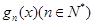 的表达式;此时若设
的表达式;此时若设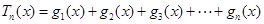 ,且关于
,且关于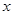 的函数
的函数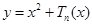
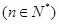 在区间
在区间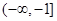 上的最小值为
上的最小值为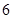 ,则求
,则求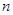 的值;
的值;
(2)设数列 为等比数列,数列
为等比数列,数列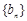 满足
满足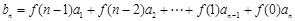 ,
,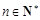 ,若
,若
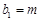 ,
,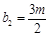 ,其中
,其中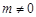 ,则
,则
①当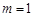 时,求
时,求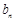 ;
;
②设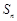 为数列
为数列 的前
的前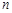 项和,若对于任意的正整数
项和,若对于任意的正整数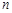 ,都有
,都有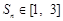 ,求实数
,求实数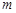 的取值范围.
的取值范围.
【答案】
①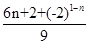 ②
②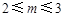
【解析】(I)先分别求出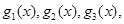 从而归纳出
从而归纳出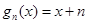 ,所以
,所以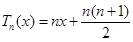 .这样可得到
.这样可得到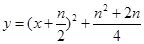 .
.
然后再讨论二次函数的对称轴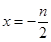 与-1的大小关系即可.
与-1的大小关系即可.
(2)在(1)的基础上,可得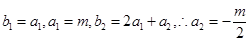 ,所以数列
,所以数列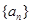 的公比为
的公比为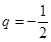 ,当m=1时,
,当m=1时,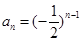 ,所以
,所以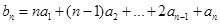 ,
,
所以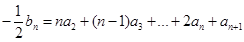 ,然后两式作差整理可得
,然后两式作差整理可得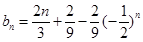 ,问题到此基本得以解决.
,问题到此基本得以解决.
解:(1)∵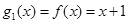 ,
,
∴
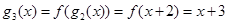 .…1分
.…1分
∴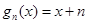 .………………2分
.………………2分
∴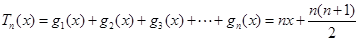 .
.
∴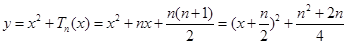 .…………4分
.…………4分
ⅰ)当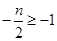 ,即
,即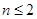 时,函数
时,函数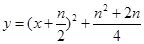 在区间
在区间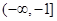 上是减函数,
上是减函数,
∴当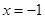 时,
时,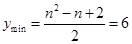 ,即
,即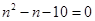 ,该方程没有整数解.…5分
,该方程没有整数解.…5分
ⅱ)当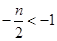 ,即
,即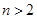 时,
时,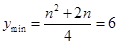 ,解得
,解得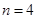 ,综上所述,
,综上所述,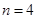 .…6分;
.…6分;
(2)①由已知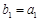 ,所以
,所以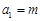 ;
;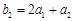 ,所以
,所以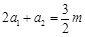 ,解得
,解得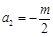 ;
所以数列
;
所以数列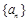 的公比
的公比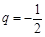 ;
....7分当
;
....7分当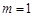 时,
时,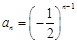 ,
, ,即
,即 …①
…①  ,………②,
,………②,
②-①得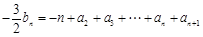 ,
,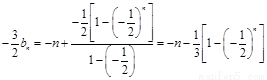 ,....8分
,....8分
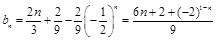 .....9分
.....9分
②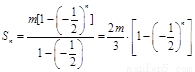 .....10分
.....10分
因为 ,所以由
,所以由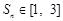 得
得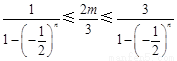 ,....11分
,....11分
注意到,当n为奇数时, ;
;
当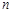 为偶数时,
为偶数时, ,
,
所以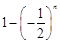 最大值为
最大值为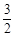 ,最小值为
,最小值为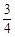 .....13分
.....13分
对于任意的正整数n都有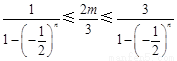 ,
,
所以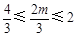 ,解得
,解得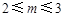 ...14分
...14分

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
 在(0,
在(0,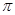 )内有两个零点
)内有两个零点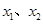 ,求
,求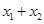 的值;
的值;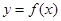 的图像向左移动
的图像向左移动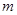
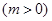 个单位,再向下平移2个单位,使所得函数的图象关于
个单位,再向下平移2个单位,使所得函数的图象关于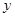 轴对称,求
轴对称,求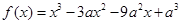 .
.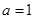 ,求函数
,求函数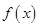 的极值;
的极值;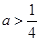 ,且当
,且当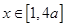 时,
时,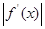
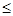 12a恒成立,试确定
12a恒成立,试确定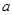 的取值范围.
的取值范围.