题目内容
（1）函数y=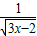
+lg（2x-1）的定义域（2）计算
．
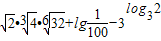【答案】分析：（1）令被开方数大于0，同时对数的真数大于0；列出不等式组，求出x的范围即为定义域．
（2）结合有理数指数幂与根式的转化关系，及对数的运算性质，求出每一项的值，即可得到答案．
解答：解：（1）要使函数有意义，需
解得：x＞
故函数的定义域为（
，+∞）
（2）原式=
+lg10-2-2=
-2-2=4-2-2=0
点评：本题考查的知识点是有理数指数幂的化简求值，对数的运算性质，其中熟练掌握有理数指数幂与根式的转化关系，将根式转化为有理数指数幂是解答本题的关键．
（2）结合有理数指数幂与根式的转化关系，及对数的运算性质，求出每一项的值，即可得到答案．
解答：解：（1）要使函数有意义，需
解得：x＞
故函数的定义域为（
，+∞）（2）原式=
+lg10-2-2=-2-2=4-2-2=0点评：本题考查的知识点是有理数指数幂的化简求值，对数的运算性质，其中熟练掌握有理数指数幂与根式的转化关系，将根式转化为有理数指数幂是解答本题的关键．
练习册系列答案
相关题目
+lg（2x-1）的定义域
．