题目内容
已知向量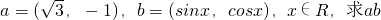 的最大值,并求使
的最大值,并求使 •
• 取得最大值时
取得最大值时 与
与 的夹角.
的夹角.
解:∵ •
• =
= sinx-cosx=2sin(x-
sinx-cosx=2sin(x- ),…(2分)
),…(2分)
∴当sin(x- )=1,即x=2kπ+
)=1,即x=2kπ+ (k∈Z)时,
(k∈Z)时,
 •
• 取得最大值2…(6分)
取得最大值2…(6分)
此时 =(
=( ,-
,- ),故cos<
),故cos< ,
, >=
>= =1,
=1,
∴ 与
与 的夹角是0…(12分)
的夹角是0…(12分)
分析:利用向量的坐标运算公式可求得 •
• =2sin(x-
=2sin(x- ),利用正弦函数的性质可求得
),利用正弦函数的性质可求得 •
• 的最大值及其取得最大值时
的最大值及其取得最大值时 与
与 的夹角.
的夹角.
点评:本题考查平面向量数量积的运算,考查三角函数的恒等变换及化简求值,属于基础题.
 •
• =
= sinx-cosx=2sin(x-
sinx-cosx=2sin(x- ),…(2分)
),…(2分)∴当sin(x-
 )=1,即x=2kπ+
)=1,即x=2kπ+ (k∈Z)时,
(k∈Z)时, •
• 取得最大值2…(6分)
取得最大值2…(6分)此时
 =(
=( ,-
,- ),故cos<
),故cos< ,
, >=
>= =1,
=1,∴
 与
与 的夹角是0…(12分)
的夹角是0…(12分)分析:利用向量的坐标运算公式可求得
 •
• =2sin(x-
=2sin(x- ),利用正弦函数的性质可求得
),利用正弦函数的性质可求得 •
• 的最大值及其取得最大值时
的最大值及其取得最大值时 与
与 的夹角.
的夹角.点评:本题考查平面向量数量积的运算,考查三角函数的恒等变换及化简求值,属于基础题.

练习册系列答案
相关题目

 的最大值,并求使
的最大值,并求使
 取得最大值时
取得最大值时 与
与 的夹角.
的夹角.