题目内容
7.与圆(x+1)2+(y-1)2=4关于直线x-y=1对称的圆的方程是(x-2)2+(y+2)2=4.分析 求出圆(x+1)2+(y-1)2=4的圆心为点C(-1,1),半径为2,因此所求圆的圆心为点C关于x-y=1对称点,圆半径为2,由此结合圆的标准方程即可得到所求圆的方程.
解答 解:∵圆(x+1)2+(y-1)2=4的圆心为点C(-1,1),半径为2,
∴已知圆关于直线x-y=1对称的圆半径为2,
设圆心C关于直线x-y=1对称的点P(a,b),则$\left\{\begin{array}{l}{\frac{b-1}{a+1}=-1}\\{\frac{a-1}{2}-\frac{b+1}{2}=1}\end{array}\right.$,
解得:a=2,b=-2,
∴P(2,-2)
因此,所求圆的标准方程为(x-2)2+(y+2)2=4.
故答案为:(x-2)2+(y+2)2=4.
点评 本题给出圆的方程,求它关于定直线对称的圆的方程,着重考查了圆的标准方程、直线与圆的位置关系等知识,属于基础题.

练习册系列答案
 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案
相关题目
18.从某学习小组的5名男生和4名女生中任意选取3名学生进行视力检测,其中至少要选到男生与女生各一名,则不同的选取种数有( )
| A. | 35 | B. | 70 | C. | 80 | D. | 140 |
17.函数y=sin2x的图象平移向量($\frac{π}{3}$,0)后,新图象对应的函数为y=( )
| A. | sin(2x-$\frac{2π}{3}$) | B. | sin(2x+$\frac{π}{3}$) | C. | sin(2x+$\frac{2π}{3}$) | D. | sin(2x-$\frac{π}{3}$) |
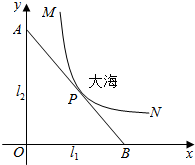 某沿海城市的海边有两条相互垂直的直线型公路l1、l2,海岸边界MPN近似地看成一条曲线段.为开发旅游资源,需修建一条连接两条公路的直线型观光大道AB,且直线AB与曲线MPN有且仅有一个公共点P(即直线与曲线相切),如图所示.若曲线段MPN是函数$y=\frac{a}{x}$图象的一段,点M到l1、l2的距离分别为8千米和1千米,点N到l2的距离为10千米,以l1、l2分别为x、y轴建立如图所示的平面直角坐标系xOy,设点P的横坐标为p.
某沿海城市的海边有两条相互垂直的直线型公路l1、l2,海岸边界MPN近似地看成一条曲线段.为开发旅游资源,需修建一条连接两条公路的直线型观光大道AB,且直线AB与曲线MPN有且仅有一个公共点P(即直线与曲线相切),如图所示.若曲线段MPN是函数$y=\frac{a}{x}$图象的一段,点M到l1、l2的距离分别为8千米和1千米,点N到l2的距离为10千米,以l1、l2分别为x、y轴建立如图所示的平面直角坐标系xOy,设点P的横坐标为p.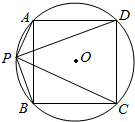 已知:如图,⊙O是正方形ABCD的外接圆,P是$\widehat{AB}$上的一点,求证:$\frac{PA+PC}{PB+PD}$=$\frac{PD}{PC}$.
已知:如图,⊙O是正方形ABCD的外接圆,P是$\widehat{AB}$上的一点,求证:$\frac{PA+PC}{PB+PD}$=$\frac{PD}{PC}$.