题目内容
某产品在某零售摊位上的零售价x(单位：元)与每天的销售量y(单位：个)的统计资料如下表所示：
| x | 16 | 17 | 18 | 19 |
| y | 50 | 34 | 41 | 31 |
由上表可得回归直线方程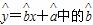
＝－4，据此模型预计零售价定为15元时，每天的销售量为( )
A．48个 B．49个
C．50个 D．51个
B
B．±
D．无法求解
已知x，y的取值如下表：
| x | 0 | 1 | 4 | 5 | 6 | 8 |
| y | 1.3 | 1.8 | 5.6 | 6.1 | 7.4 | 9.3 |
从所得的散点图分析可知：y与x线性相关，且
＝0.95x＋a，则a＝( )
A．1.30 B．1.45
C．1.65 D．1.80
在2012年8月15日那天，某市物价部门对本市的5家商场的某商品的一天销售量及其价格进行调查，5家商场的售价x元和销售量y件之间的一组数据如下表所示：
| 价格x | 9 | 9.5 | m | 10.5 | 11 |
| 销售量y | 11 | n | 8 | 6 | 5 |
由散点图可知，销售量y与价格x之间有较强的线性相关关系，其线性回归直线方程是：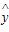
＝－3.2x＋40，且m＋n＝20，则其中的n＝________.
某车间为了规定工时定额，需要确定加工零件所花费的时间，为此作了四次试验，得到的数据如下：
| 零件的个数x(个) | 2 | 3 | 4 | 5 |
| 加工的时间y(小时) | 2.5 | 3 | 4 | 4.5 |
(1)在给定的坐标系中画出表中数据的散点图；
(2)求出y关于x的线性回归方程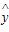＝bx＋a，并在坐标系中画出回归直线；
(3)试预测加工10个零件需要多少时间？
(注：b＝
，a＝
－b
)
的概率是( )
B.
D.