题目内容
把边长为a的正三角形ABC沿高线AD折成60°的二面角,点A到BC的距离是
- A.a
- B.
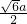
- C.

- D.

D
分析:此题是“折叠问题”,需抓住不变的量:AD⊥BD,AD⊥DC,BD∩DC=D,所以AD⊥面BDC,则由三垂线定理可过点D作DQ⊥BC,垂足为Q,连接AQ,则点A到BC的距离即为AQ的长度,且∠BDC=60°.
解答: 解:如图,过点D作DQ⊥BC,垂足为Q,连接AQ
解:如图,过点D作DQ⊥BC,垂足为Q,连接AQ
∵AD⊥BD,AD⊥DC,BD∩DC=D
∴AD⊥面BDC
∴根据三垂线定理可得:AQ⊥BC,则点A到BC的距离即为AQ的长度
∵AD⊥BD,AD⊥DC,
∴∠BDC=60°
又∵BD=DC= ,
,
∴∠QDC=30°
在Rt△QDC中,DQ=DC•cos30°=
又∵AD=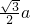
∴在Rt△ADQ中,AQ=
故选D.
点评:本小题考查空间中的线面关系,二面角的平面角、解三角形等基础知识考查空间想象能力和思维能力.
分析:此题是“折叠问题”,需抓住不变的量:AD⊥BD,AD⊥DC,BD∩DC=D,所以AD⊥面BDC,则由三垂线定理可过点D作DQ⊥BC,垂足为Q,连接AQ,则点A到BC的距离即为AQ的长度,且∠BDC=60°.
解答:
 解:如图,过点D作DQ⊥BC,垂足为Q,连接AQ
解:如图,过点D作DQ⊥BC,垂足为Q,连接AQ∵AD⊥BD,AD⊥DC,BD∩DC=D
∴AD⊥面BDC
∴根据三垂线定理可得:AQ⊥BC,则点A到BC的距离即为AQ的长度
∵AD⊥BD,AD⊥DC,
∴∠BDC=60°
又∵BD=DC=
 ,
,∴∠QDC=30°
在Rt△QDC中,DQ=DC•cos30°=

又∵AD=
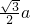
∴在Rt△ADQ中,AQ=

故选D.
点评:本小题考查空间中的线面关系,二面角的平面角、解三角形等基础知识考查空间想象能力和思维能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
把边长为a的正三角形ABC沿高线AD折成60°的二面角,点A到BC的距离是( )
| A、a | ||||
B、
| ||||
C、
| ||||
D、
|


