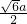题目内容
把边长为a的正三角形ABC沿AB边的高线折成60°的二面角, 这时A到BC的距离是[ ]
A.
a B.
a C.
a D.
a
答案：C
解析：
解析：
|
解: 如图, CD是AB边上的高. 过A＇作BD边的垂线A＇E, 垂足为E. 因为 CD⊥A＇D, CD⊥BD.
所以∠A＇DB＝60°, DE＝ 所以 CD⊥平面A＇DB. 所以CD⊥A＇E. 所以 A＇E⊥平面BCD 过E作EF⊥BC交BC于F. 连结A＇F, 由三垂线定理知A＇F⊥BC.
EF＝
|
, A＇E＝
a 
·sin60°＝
a
练习册系列答案
相关题目
把边长为a的正三角形ABC沿高线AD折成60°的二面角，点A到BC的距离是（ ）
| A、a | ||||
B、
| ||||
C、
| ||||
D、
|
