题目内容
已知动圆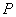 过定点
过定点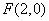 且与直线
且与直线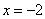 相切,圆心
相切,圆心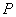 的轨迹为曲线
的轨迹为曲线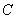
(I)求轨迹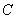 的方程;
的方程;
(Ⅱ)①过定点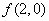 作互相垂直的直线
作互相垂直的直线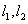 分别交轨迹
分别交轨迹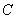 于点
于点 和点
和点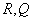 ,求四边形
,求四边形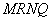 面积的最小值;
面积的最小值;
②定点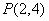 ,动点
,动点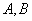 是轨迹
是轨迹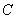 上的三个点,且满足
上的三个点,且满足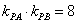 试问
试问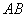 所在的直线是否过定点,若是,求出该定点的坐标;否则说明理由
所在的直线是否过定点,若是,求出该定点的坐标;否则说明理由
解:(1)由题意: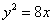 为点M的轨迹方程。
为点M的轨迹方程。
(2)由题易知直线l1,l2的斜率都存在,且不为0,
不妨设,MN方程为y=k(x-2)与y2=8x联立得:
k2x2-(4k2+8)x+4k2=0,设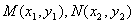
∴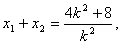
由抛物线定义知:|MN|=|MF|+|NF|
同理RQ的方程为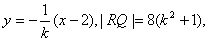
∴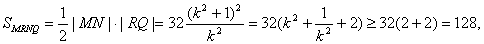
当且仅当k2=1,k=±1时取“=”,故四边形MRNQ的面积的最小值为128.
(3)设
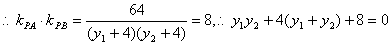 ········(※)
········(※)
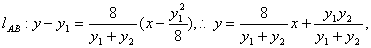
则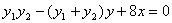 ,与(※)比较可知,直线AB过定点(1,-4)
,与(※)比较可知,直线AB过定点(1,-4)
法2:
设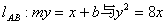 联立得:
联立得: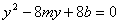 由△>0得2m2>b。
由△>0得2m2>b。
设y1+y2=8m,y1·y2=8b,又由kPA·kPB=8
即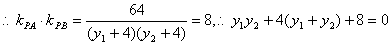
∴4m+b+1=0
∴lAB:my=x-4m-1即m(y+4)=x-1,∴直线AB过定点(1,-4)

练习册系列答案
相关题目
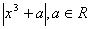 在[-1,1]上的最大值为M(a) ,若函数g(x)=M(x)-
在[-1,1]上的最大值为M(a) ,若函数g(x)=M(x)-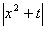 有4个零点,则实数t的取值范围为。
有4个零点,则实数t的取值范围为。 ) B. (
) B. (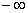 1, -1) C. (
1, -1) C. (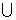 (1,
(1, 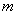 ),则这个几何体的体积为__________
),则这个几何体的体积为__________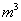
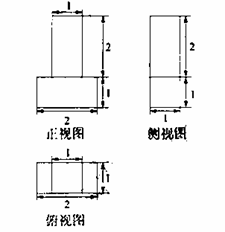
 上存在不同的三点到原点的距离构成等比数列,则该公比不可能是( )
上存在不同的三点到原点的距离构成等比数列,则该公比不可能是( ) B.
B. C.
C. D.
D.
 满足:
满足: ,且
,且
 ;
; 中:
中: ,求数列
,求数列 的前20项和.
的前20项和.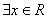 ,使得x2+x+1<0”,则
,使得x2+x+1<0”,则
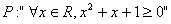
 的前
的前 项和为
项和为 ,且
,且 ,则
,则 _____.
_____. 的定义域为
的定义域为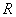 ,若存在常数
,若存在常数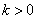 ,使
,使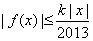 对于一切
对于一切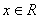 均成立,则称
均成立,则称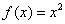 ; ②
; ②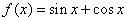 ;
; 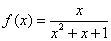 ; ④
; ④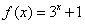 。其中
。其中