题目内容
已知两条直线L1:x+y-1=0,L2:2x-y+4=0的交点为P,动直线L:ax-y-2a+1=0.
(1)若直线L过点P,求实数a的值.
(2)若直线L与直线L1垂直,求三条直线L,L1,L2 围成的三角形的面积.
(1)若直线L过点P,求实数a的值.
(2)若直线L与直线L1垂直,求三条直线L,L1,L2 围成的三角形的面积.
考点:直线的一般式方程与直线的垂直关系,点到直线的距离公式
专题:直线与圆
分析:(1)由
,求出P(-1,2),把P(-1,2)代入直线l:ax-y-2a+1=0,能求出a.
(2)由直线l⊥l1,得a=1,解方程组求出B(1,0),C(-5,-6),由此能求出△PBC的面积.
|
(2)由直线l⊥l1,得a=1,解方程组求出B(1,0),C(-5,-6),由此能求出△PBC的面积.
解答:
解:(1)由
,解得
,
∴P(-1,2),把P(-1,2)代入直线l:ax-y-2a+1=0,
解得a=-
.
(2)∵直线l⊥l1,∴a=1,
设直线l与l1交于B,直线l与l2交于C,
∴
,解得
,∴B(1,0),
同理,由
,解得
,∴C(-5,-6),
∴PB=2
,BC=6
,
∴△PBC的面积为S=
×2
×6
=12.
|
|
∴P(-1,2),把P(-1,2)代入直线l:ax-y-2a+1=0,
解得a=-
| 1 |
| 3 |
(2)∵直线l⊥l1,∴a=1,
设直线l与l1交于B,直线l与l2交于C,
∴
|
|
同理,由
|
|
∴PB=2
| 2 |
| 2 |
∴△PBC的面积为S=
| 1 |
| 2 |
| 2 |
| 2 |
点评:本题考查实数的求法,考查三角形面积的求法,解题时要认真审题,是基础题.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
命题“如果x≤2mn,那么x≤m2+n2”的逆否命题是( )
| A、如果x>2mn,那么x≥m2+n2 |
| B、如果x≥m2+n2,那么x≥2mn |
| C、如果x>m2+n2,那么x>2mn |
| D、如果x<2mn,那么x≤m2+n2 |

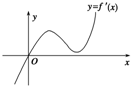 定义在R上的函数f(x)满足f(4)=1,f′(x)为f(x)的导函数,已知函数y=f′(x)的图象如图所示.若两正数a,b满足f(2a+b)<1,则
定义在R上的函数f(x)满足f(4)=1,f′(x)为f(x)的导函数,已知函数y=f′(x)的图象如图所示.若两正数a,b满足f(2a+b)<1,则
