题目内容
9.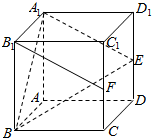 如图所示,在正方体ABCD-A1B1C1D1中,点E、F分别是棱DD1、CC1的中点.
如图所示,在正方体ABCD-A1B1C1D1中,点E、F分别是棱DD1、CC1的中点.(I)求证:直线B1F∥平面A1BE;
(Ⅱ)求直线BE和平面ABB1A1所成的角的正弦值.
分析 (I)连接EF,则四边形EFB1 A1为平行四边形,从而B1F∥A1E,由此能证明直线B1F∥平面A1BE.
(II)取AA1的中点M,连接EM,BM,推导出∠EBM即为直线BE与平面ABB1A1所成的角,由此能求出直线BE和平面ABB1A1所成的角的正弦值.
解答  证明:(I)如图1,连接EF,由点E、F分别是棱DD1、CC1的中点,
证明:(I)如图1,连接EF,由点E、F分别是棱DD1、CC1的中点,
则在正方体ABCD-A1B1C1D1中,EF∥C1D1,且EF=C1D1,A1B1∥C1D1,且A1B1=C1D1,
所以EF∥A1B1,且EF=A1B1,
所以四边形EFB1A1为平行四边形,所以B1F∥A1E,
而A1E⊆平面A1BE,B1F?平面平面A1BE,
所以直线B1F∥平面A1BE.…(5分)
解:(II)如图2,取AA1的中点M,连接EM,BM,
因为E是DD1的中点,四边形ADD1A1为正方形,所以EM∥AD,
又在正方体ABCD-A1B1C1D1中,AD⊥平面ABB1A1,
所以EM⊥ABB1A1,从而BM为直线BE在平面ABB1A1上的射影,
所以∠EBM即为直线BE与平面ABB1A1所成的角.
设正方体的棱长为2,则EM=AD=2,BE=$\sqrt{{2}^{2}+{2}^{2}+{1}^{2}}$=3.
于是,在Rt△BEM中,sin∠EBM=$\frac{EM}{BE}$=$\frac{2}{3}$.
即直线BE和平面ABB1A1所成的角的正弦值为$\frac{2}{3}$.…(12分)
点评 本题考查线面平行的证明,考查线面角的正弦值的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
6.从6名学生中选出2名学生担任数学、物理课代表的选法有( )
| A. | 10种 | B. | 15种 | C. | 30种 | D. | 45种 |
3.与圆x2+y2-x+2y=0关于直线x-y+1=0对称的圆的方程为( )
| A. | (x-2)2+(y-$\frac{3}{2}$)2=$\frac{5}{4}$ | B. | (x+2)2+(y-$\frac{3}{2}$)2=$\frac{5}{4}$ | C. | (x+2)2+(y+$\frac{3}{2}$)2=$\frac{5}{4}$ | D. | (x-2)2+(y+$\frac{3}{2}$)2=$\frac{5}{4}$ |
14. 如图,已知正三棱锥P-ABC中,底面是正三角形,P在底面内的射影是正三角形的中心.若AB=1,侧面和底面所成的角是60°,则此棱锥的表面积是( )
如图,已知正三棱锥P-ABC中,底面是正三角形,P在底面内的射影是正三角形的中心.若AB=1,侧面和底面所成的角是60°,则此棱锥的表面积是( )
 如图,已知正三棱锥P-ABC中,底面是正三角形,P在底面内的射影是正三角形的中心.若AB=1,侧面和底面所成的角是60°,则此棱锥的表面积是( )
如图,已知正三棱锥P-ABC中,底面是正三角形,P在底面内的射影是正三角形的中心.若AB=1,侧面和底面所成的角是60°,则此棱锥的表面积是( )| A. | $\frac{3\sqrt{3}}{4}$ | B. | $\frac{5\sqrt{3}}{4}$ | C. | $\frac{1}{4}$+$\frac{\sqrt{3}}{2}$ | D. | $\frac{1}{2}$+$\frac{\sqrt{3}}{4}$ |
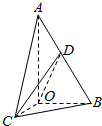 如图,在Rt△AOB中,∠OAB=30°,斜边AB=4,将△AOB绕直线AO旋转得到△AOC,且二面角B-AO-C是直二面角,动点D在边AB上.
如图,在Rt△AOB中,∠OAB=30°,斜边AB=4,将△AOB绕直线AO旋转得到△AOC,且二面角B-AO-C是直二面角,动点D在边AB上.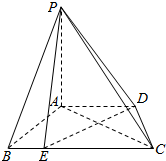 如图,在四棱锥P-ABCD中,PA⊥面ABCD,AB⊥AD,BC∥AD,AP=$\sqrt{2}$,AB=AD=1,BC=2,$\overrightarrow{BE}=\frac{1}{4}\overrightarrow{BC}$.
如图,在四棱锥P-ABCD中,PA⊥面ABCD,AB⊥AD,BC∥AD,AP=$\sqrt{2}$,AB=AD=1,BC=2,$\overrightarrow{BE}=\frac{1}{4}\overrightarrow{BC}$.