Question

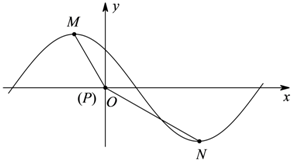（2012•焦作模拟）函数y=

3

sin（

π

4

x+?），|?|＜π的一部分图象如图所示，其中M(-1，

3

)，N(3，-

3

)为图象的两极值点．
（Ⅰ）求φ的值；
（Ⅱ）设∠MPN=β，其中P与坐标原因O重合，0≤β≤π，求tan（φ-β）的值．

Answer 1

分析：（Ⅰ）由于点M、N分别是函数的图象上的最高点和最低点，再由五点法作图可得

π

4

×(-1)+∅=

π

2

，由此求得∅的值．
（Ⅱ）如图由余弦定理求得cosβ=- 

3

2

，再由β的范围求出β的值，从而得到?-β=-

π

12

，利用tan(?-β)=-tan

π

12

=-tan(

π

4

-

π

6

) 以及两角差的正切公式求得结果．

解答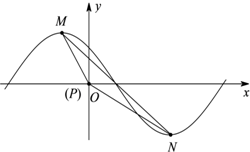：解：（Ⅰ）∵点M、N分别是函数的图象上的最高点和最低点，由五点法作图可得
∴

π

4

×(-1)+∅=

π

2

，∅=

3π

4

． …（4分）
（Ⅱ）如图，△ABC中，由余弦定理得 cosβ=

|PM|2+|PN|2-|MN|2

2|PM||PN|

=

4+12-28

8 3

=-

3

2

，cosβ=

|PM|2+|PN|2-|MN|2

2|PM||PN|

=

4+12-28

8 3

=-

3

2

又∵0≤β≤π，∴β=

5

6

π．…（9分）
∴?-β=-

π

12

，
∴tan(?-β)=-tan

π

12

=-tan(

π

4

-

π

6

)=

tan π 4 -tan π 6

1+tan π 4 •tan π 6

=-2+

3

．…（12分）

点评：本题主要考查由函数y=Asin（ωx+∅）的部分图象求解析式，余弦定理、以及查两角差的正切公式的应用，属于中档题．