题目内容
7.如图,平行四边形ABCD中,$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,M是DC的中点,以$\overrightarrow{a}$,$\overrightarrow{b}$为基底表示向量$\overrightarrow{AM}$=$\frac{1}{2}$$\overrightarrow{a}$$+\overrightarrow{b}$.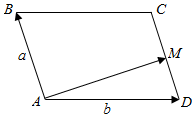
分析 根据平行四边形的概念及相等向量的概念便得到$\overrightarrow{DC}=\overrightarrow{AB}=\overrightarrow{a}$,而根据向量加法和数乘的几何意义便可得出$\overrightarrow{AM}=\frac{1}{2}\overrightarrow{a}+\overrightarrow{b}$.
解答 解:根据条件$\overrightarrow{DC}=\overrightarrow{AB}=\overrightarrow{a}$,$\overrightarrow{AM}=\overrightarrow{AD}+\overrightarrow{DM}=\overrightarrow{AD}+\frac{1}{2}\overrightarrow{DC}$=$\frac{1}{2}\overrightarrow{a}+\overrightarrow{b}$.
故答案为:$\frac{1}{2}\overrightarrow{a}+\overrightarrow{b}$.
点评 考查平行四边形的概念,相等向量的概念,以及向量的加法和数乘的几何意义,清楚向量基底的概念.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.已知全集$U=\left\{{\left.y\right|y={{log}_2}x,x=\frac{1}{2},1,2,16}\right\}$,集合A={-1,1},B={1,4},则A∩(∁UB)=( )
| A. | {-1,1} | B. | {-1} | C. | {1} | D. | ∅ |
19.设tan(3π+θ)=a,则$\frac{sin(θ-5π)+cos(π-θ)}{sin(-θ)-cos(π+θ)}$的值为( )
| A. | $\frac{a+1}{a-1}$ | B. | $\frac{a-1}{a+1}$ | C. | $\frac{-a-1}{a-1}$ | D. | $\frac{-a+1}{a-1}$ |