题目内容
6.连续抛掷同一颗均匀的骰子,令第i次得到的点数为ai,若存在正整数k,使a1+a2+…+ak=6,则称k为你的幸运数字.则你的幸运数字为3的概率$\frac{5}{108}$.分析 设“连续抛掷k次骰子,和为6”为事件A,则它包含事件A1、A2,A3,其中A1:三次恰好均为2;A2:三次中恰好1,2,3各一次.A3:三次中有两次均为1,一次为4,A1,A2为互斥事件,由此能求出k=3的概率.
解答 解:设“连续抛掷k次骰子,和为6”为事件A,则它包含事件A1、A2,A3,
其中A1:三次恰好均为2;A2:三次中恰好1,2,3各一次.A3:三次中有两次均为1,一次为4,
A1,A2为互斥事件,则k=3的概率:
P(A)=P(A1)+P(A2)+P(A3)=${C}_{3}^{3}(\frac{1}{6})^{3}$+${C}_{3}^{1}•\frac{1}{6}•{C}_{2}^{1}•\frac{1}{6}•{C}_{1}^{1}•\frac{1}{6}$+${C}_{3}^{2}(\frac{1}{6})^{2}•\frac{1}{6}$=$\frac{5}{108}$,
故答案为:$\frac{5}{108}$
点评 本题考查概率的求法,解题时要认真审题,注意互斥事件概率加法公式的合理运用.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
16.已知直线l的倾斜角为α,斜率为k,那么“$α>\frac{π}{3}$”是“$k>\sqrt{3}$”的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
1.如图可能是下列哪个函数的图象( )
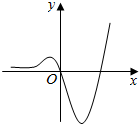

| A. | y=2x-x2-1 | B. | y=$\frac{x}{lnx}$ | C. | y=$\frac{{2}^{x}sinx}{{4}^{x}+1}$ | D. | y=(x2-2x)ex |
18.M是椭圆$\frac{{x}^{2}}{8}$+$\frac{{y}^{2}}{4}$=1上一点,F1,F2是椭圆的左、右焦点,I是△MF1F2的内心,延长MI交F1F2于N,则$\frac{|MI|}{|IN|}$等于( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\sqrt{2}$ | C. | 2 | D. | 1 |
15.设α:x=1且y=2,β:x+y=3,α是β成立的( )
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 既非充分又非必要条件 |