题目内容
如下图,已知正方形ABCD的对角线AC在直线x+2y-1=0上,且顶点A(-5,3)、B(a,0)(a>-5),求顶点B、C、D的坐标.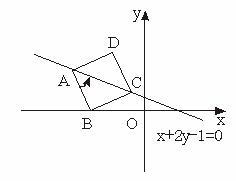
解:∵A(-5,3)、B(a,0)(a>-5),
∴kAB=![]() .而kAC=-
.而kAC=-![]() ,
,
又AB到AC的角为45°,∴tan45°=![]() =
= =1,即
=1,即![]() =1.解得a=-4.故
=1.解得a=-4.故
B(-4,0).
又点C在AC上,可设C(1-2b,b),
∵BC⊥AB,kAB·kBC=-1,∴(-3)·![]() =-1.解得b=1.故C(-1,1).
=-1.解得b=1.故C(-1,1).
设D(x,y),∵BD中点与AC中点重合,
∴ ∴
∴![]() 故D(-2,4).
故D(-2,4).
综上,所求顶点B、C、D的坐标分别是(-4,0),(-1,1),(-2,4).
点评:综合使用解析几何知识和平面几何性质是解决本题的关键.

练习册系列答案
相关题目
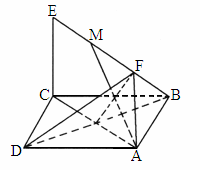
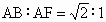 ,M为线段EF的中点.
,M为线段EF的中点.