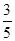题目内容
过点(0,1)引x2+y2-4x+3=0的两条切线,这两条切线夹角的余弦值为( )A.

B.

C.

D.
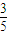
【答案】分析:(法一):设切线饿方程为kx-y+1=0,由切线的性质可得,圆心(2,0)到直线kx-y+1=0的距离d=1可求k,设两直线的夹角为α,代入夹角公式可先求tanα,然后结合同角基本关系可求cosα
(法二):由A(0,1)在圆外可得过A(0,1做圆的切线可作两条AM,AN,圆心C(2,0),则AM⊥CM,AN⊥CN,∠CAM=∠CAN=β,由两点间的距离公式可求AC,CM=1,从而有AM2=AC2-CM2,进而可求cosβ=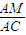 ,由二倍角的余弦公式cos2β=2cos2β-1可求
,由二倍角的余弦公式cos2β=2cos2β-1可求
解答:解:(法一)设切线饿方程为y-1=kx即kx-y+1=0
由切线的性质可得,圆心(2,0)到直线kx-y+1=0的距离d=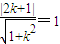
∴k=0或k=-
设两直线的夹角为α,则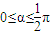
由直线的夹角公式可得,tanα=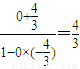
∵1+tan2α=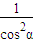 =
=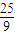 ,cosα>0
,cosα>0
∴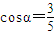
(法二):由A(0,1)在圆外可得过A(0,1做圆的切线可作两条AM,AN,圆心C(2,0),连接CM,CN,AC
则AM⊥CM,AN⊥CN,∠CAM=∠CAN=β,AC=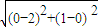 =
= ,CM=1
,CM=1
在Rt△ACM中,AM2=AC2-CM2=2,cosβ=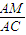 =
=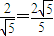
∴cos2β=2cos2β-1=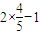 =
=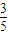
故选:D
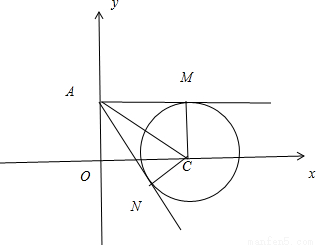
点评:本题主要考查了直线的夹角公式的应用,解法(一)中主要是利用直线与圆相切的性质求解出切线的斜率,解法(二)主要是利用了基本图形及二倍角的余弦.
(法二):由A(0,1)在圆外可得过A(0,1做圆的切线可作两条AM,AN,圆心C(2,0),则AM⊥CM,AN⊥CN,∠CAM=∠CAN=β,由两点间的距离公式可求AC,CM=1,从而有AM2=AC2-CM2,进而可求cosβ=
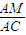 ,由二倍角的余弦公式cos2β=2cos2β-1可求
,由二倍角的余弦公式cos2β=2cos2β-1可求解答:解:(法一)设切线饿方程为y-1=kx即kx-y+1=0
由切线的性质可得,圆心(2,0)到直线kx-y+1=0的距离d=
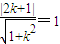
∴k=0或k=-

设两直线的夹角为α,则
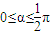
由直线的夹角公式可得,tanα=
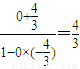
∵1+tan2α=
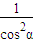 =
=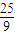 ,cosα>0
,cosα>0∴
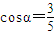
(法二):由A(0,1)在圆外可得过A(0,1做圆的切线可作两条AM,AN,圆心C(2,0),连接CM,CN,AC
则AM⊥CM,AN⊥CN,∠CAM=∠CAN=β,AC=
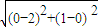 =
= ,CM=1
,CM=1在Rt△ACM中,AM2=AC2-CM2=2,cosβ=
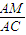 =
=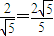
∴cos2β=2cos2β-1=
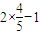 =
=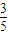
故选:D

点评:本题主要考查了直线的夹角公式的应用,解法(一)中主要是利用直线与圆相切的性质求解出切线的斜率,解法(二)主要是利用了基本图形及二倍角的余弦.

练习册系列答案
相关题目
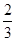 B.
B.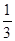 C.
C.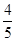 D.
D.