题目内容
已知椭圆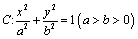 过点
过点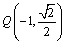 ,且离心率
,且离心率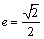 .
.
(I)求椭圆C的方程;
(II)已知过点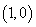 的直线
的直线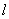 与该椭圆相交于A、B两点,试问:在直线
与该椭圆相交于A、B两点,试问:在直线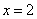 上是否存在点P,使得
上是否存在点P,使得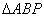 是正三角形?若存在,求出点P的坐标;若不存在,请说明理由.
是正三角形?若存在,求出点P的坐标;若不存在,请说明理由.
解:(Ⅰ)由题意得 ……2分 解得
……2分 解得 …………………4分
…………………4分
所以椭圆 的方程为
的方程为 . …………………………………… 5分
. …………………………………… 5分
(Ⅱ)当直线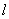 的斜率为0时,不存在符合题意的点
的斜率为0时,不存在符合题意的点 ; …………………6分
; …………………6分
当直线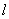 的斜率不为0时,设直线
的斜率不为0时,设直线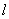 的方程为
的方程为 ,
,
代入 ,整理得
,整理得 ,
,
设 ,
, ,则
,则 ,
, ,
,
设存在符合题意的点 ,
,
则

 , …………………………………8分
, …………………………………8分
设线段 的中点
的中点 ,则
,则 ,
,
所以 ,
,
因为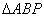 是正三角形,所以
是正三角形,所以 ,且
,且 , ……………9分
, ……………9分
由 得
得 即
即 ,所以
,所以 ,
,
所以 ,
,
……………10分
由 得
得 ,
,
解得 ,所以
,所以 .……………………………………………………12分
.……………………………………………………12分
由 得
得 ,
,
所以 ,
,
所以存在符合题意的点 .
.

练习册系列答案
相关题目
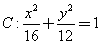 ,直线
,直线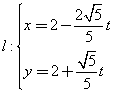 (
(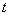 为参数)
为参数)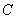 的参数方程,直线
的参数方程,直线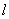 的普通方程;
的普通方程;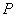 作与
作与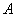 ,求
,求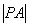 的最大值及此时P点的坐标。
的最大值及此时P点的坐标。 的公比0<q<1,
的公比0<q<1, ,则使
,则使 >
> 成立的正整数n的最大值为 .
成立的正整数n的最大值为 . 及其三视图中的正(主)视图和侧(左)视图如图所示,则棱SB的长为( )
及其三视图中的正(主)视图和侧(左)视图如图所示,则棱SB的长为( ) B.
B. C.
C. D.
D.

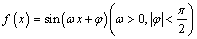 的部分图象如图所示.
的部分图象如图所示. 的解析式,并写出
的解析式,并写出 的内角分别是A,B, C,角A为锐角,且的值.
的内角分别是A,B, C,角A为锐角,且的值.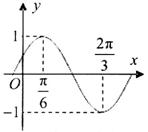
 中,若
中,若 ,数列
,数列 项积为
项积为 ,若
,若 ,则
,则 的值为 ( )
的值为 ( ) 的图像的一条对称轴为
的图像的一条对称轴为 ,则以
,则以 为方向向量的直线的倾斜角为 .
为方向向量的直线的倾斜角为 . cm,高为2 cm,AB,CD分别是两底面的直径,AD,BC是母线.若一只小虫从A点出发,从侧面爬行到C点,则小虫爬行的最短路线的长度是________cm.(结果保留根式)
cm,高为2 cm,AB,CD分别是两底面的直径,AD,BC是母线.若一只小虫从A点出发,从侧面爬行到C点,则小虫爬行的最短路线的长度是________cm.(结果保留根式)
 的底面是边长为1的正方形,
的底面是边长为1的正方形,  ,
, ,
,  为
为 上两点,且
上两点,且  .
. 面
面 ;
; 的余弦值。
的余弦值。