题目内容
设函数f(x)=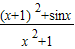 的最大值为M,最小值为m,则M+m= .
的最大值为M,最小值为m,则M+m= .
【答案】分析:函数可化为f(x)=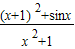 =
=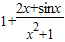 ,令
,令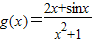 ,则
,则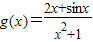 为奇函数,从而函数
为奇函数,从而函数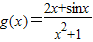 的最大值与最小值的和为0,由此可得函数f(x)=
的最大值与最小值的和为0,由此可得函数f(x)=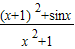 的最大值与最小值的和.
的最大值与最小值的和.
解答:解:函数可化为f(x)=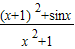 =
=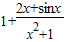
令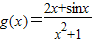 ,则
,则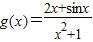 为奇函数
为奇函数
∴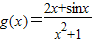 的最大值与最小值的和为0
的最大值与最小值的和为0
∴函数f(x)=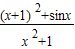 的最大值与最小值的和为1+1+0=2
的最大值与最小值的和为1+1+0=2
即M+m=2
故答案为:2
点评:本题考查函数的最值,考查函数的奇偶性,解题的关键是将函数化简,转化为利用函数的奇偶性解题.
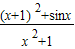 =
=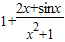 ,令
,令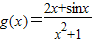 ,则
,则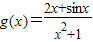 为奇函数,从而函数
为奇函数,从而函数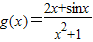 的最大值与最小值的和为0,由此可得函数f(x)=
的最大值与最小值的和为0,由此可得函数f(x)=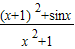 的最大值与最小值的和.
的最大值与最小值的和.解答:解:函数可化为f(x)=
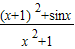 =
=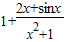
令
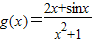 ,则
,则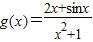 为奇函数
为奇函数∴
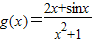 的最大值与最小值的和为0
的最大值与最小值的和为0∴函数f(x)=
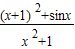 的最大值与最小值的和为1+1+0=2
的最大值与最小值的和为1+1+0=2即M+m=2
故答案为:2
点评:本题考查函数的最值,考查函数的奇偶性,解题的关键是将函数化简,转化为利用函数的奇偶性解题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
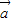 =(cosωx,2cosωx),
=(cosωx,2cosωx),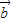 =(2cosωx,sinωx)(x∈R,ω>0),已知函数f(x)=
=(2cosωx,sinωx)(x∈R,ω>0),已知函数f(x)= +1的最小正周期是
+1的最小正周期是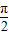 .
.