题目内容
在△ABC中, =(cos23°,cos67°),
=(cos23°,cos67°), =(2cos68°,2cos22°),则cosB=
=(2cos68°,2cos22°),则cosB=
- A.-

- B.

- C.-

- D.

C
分析:由题意可得 =-
=- ,
, =1,
=1, =2,代入向量的夹角公式cosB=
=2,代入向量的夹角公式cosB=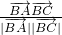 可得结果.
可得结果.
解答:∵ =(cos23°,cos67°),∴
=(cos23°,cos67°),∴ =(-cos23°,-cos67°)
=(-cos23°,-cos67°)
由数量积的定义可得: =-cos23°×2cos68°-cos67°×2cos22°
=-cos23°×2cos68°-cos67°×2cos22°
=-2(cos23°×sin22°+sin23°×cos22°)
=-2sin(23°+22°)=-2sin45°=- ,
,
而 =
= =
= =1,
=1,
 =
= =
= =2
=2
故cosB=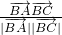 =
= =
=
故选C
点评:本题为向量夹角公式的运用,熟练掌握向量的模长公式和三角函数的运算是解决问题的关键,属中档题.
分析:由题意可得
 =-
=- ,
, =1,
=1, =2,代入向量的夹角公式cosB=
=2,代入向量的夹角公式cosB=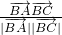 可得结果.
可得结果.解答:∵
 =(cos23°,cos67°),∴
=(cos23°,cos67°),∴ =(-cos23°,-cos67°)
=(-cos23°,-cos67°)由数量积的定义可得:
 =-cos23°×2cos68°-cos67°×2cos22°
=-cos23°×2cos68°-cos67°×2cos22°=-2(cos23°×sin22°+sin23°×cos22°)
=-2sin(23°+22°)=-2sin45°=-
 ,
,而
 =
= =
= =1,
=1, =
= =
= =2
=2故cosB=
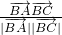 =
= =
=
故选C
点评:本题为向量夹角公式的运用,熟练掌握向量的模长公式和三角函数的运算是解决问题的关键,属中档题.

练习册系列答案
相关题目