题目内容
2．为弘扬中国传统文化，某校在高中三个年级中抽取甲、乙、丙三名同学进行问卷调查．调查结果显示这三名同学来自不同的年级，加入了不同的三个社团：“楹联社”、“书法社”、“汉服社”，还满足如下条件：（1）甲同学没有加入“楹联社”；
（2）乙同学没有加入“汉服社”；
（3）加入“楹联社”的那名同学不在高二年级；
（4）加入“汉服社”的那名同学在高一年级；
（5）乙同学不在高三年级．
试问：甲同学所在的社团是（ ）
| A． | 楹联社 | B． | 书法社 | ||
| C． | 汉服社 | D． | 条件不足无法判断 |
分析 确定乙在高二，加入“书法社”，根据（1）甲同学没有加入“楹联社”，可得甲同学所在的社团是汉服社．
解答 解：假设乙在高一，则加入“汉服社”，与（2）矛盾，
所以乙在高二，根据（3），可得乙加入“书法社”，
根据（1）甲同学没有加入“楹联社”，
可得甲同学所在的社团是汉服社，
故选C．
点评 本题考查进行简单的合情推理，考查学生分析解决问题的能力，确定乙在高二，加入“书法社”是关键．
练习册系列答案
名师导航单元期末冲刺100分系列答案
名校名卷单元同步训练测试题系列答案
相关题目
13．设正实数a，b满足a+b=1，则（ ）
| A． | $\frac{1}{a}+\frac{1}{b}$有最大值4 | B． | $\sqrt{ab}$有最小值 $\frac{1}{2}$ | C． | $\sqrt{a}+\sqrt{b}$有最大值$\sqrt{2}$ | D． | a2+b2有最小值$\frac{{\sqrt{2}}}{2}$ |
10．函数f（x）=lnx与函数g（x）=ax2-a的图象在点（1，0）的切线相同，则实数a的值为（ ）
| A． | 1 | B． | -$\frac{1}{2}$ | C． | $\frac{1}{2}$ | D． | $\frac{1}{2}$或-$\frac{1}{2}$ |
14．
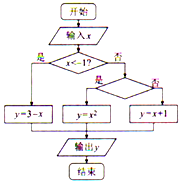已知分段函数y=$\left\{\begin{array}{l}{3-x，x＜-1}\\{{x}^{2}，-1≤x≤1}\\{x+1，x＞1}\end{array}\right.$，若执行如图所示的程序框图，则框图中的条件应该填写（ ）
已知分段函数y=$\left\{\begin{array}{l}{3-x，x＜-1}\\{{x}^{2}，-1≤x≤1}\\{x+1，x＞1}\end{array}\right.$，若执行如图所示的程序框图，则框图中的条件应该填写（ ）| A． | x≥1？ | B． | x≥-1？ | C． | -1≤x≤2？ | D． | x≤1？ |
11．数列{an}满足a1=2，an+1=$\frac{1}{{1-{a_n}}}（n∈{N^+}）$，则a2017=（ ）
| A． | -2 | B． | -1 | C． | 2 | D． | $\frac{1}{2}$ |