题目内容
15.已知函数f(x)=1-|x|+$\frac{2}{1+5{x}^{2}}$,若f(x-2)>f(3),则x的取值范围是(-1,5).分析 对函数进行判断其单调性和奇偶性,即可求解f(x-2)>f(3)x的取值范围.
解答 解:函数f(x)=1-|x|+$\frac{2}{1+5{x}^{2}}$,
则f(-x)=1-|-x|+$\frac{2}{1+5{x}^{2}}$=f(x),
故得f(x)是偶函数.
又∵y=-|x|是减函数,y=$\frac{2}{1+5{x}^{2}}$也是减函数
∴函数f(x)=1-|x|+$\frac{2}{1+5{x}^{2}}$在定义域内是减函数.
故f(x-2)>f(3)等价于(x-2)2<32,
解得:-1<x<5.
∴不等式的解集为{x|-1<x<5}.
故答案为:(-1,5).
点评 本题主要考查了函数的奇偶性和单调性判断及其运用能力.属于基础题.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案
相关题目
5.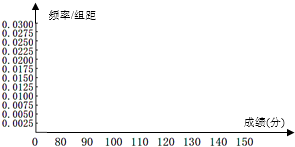 某市十所重点中学进行高二联考共有5000名学生,为了了解数学学科的学习情况,现从中随机的抽取若干名学生在这次测试中的数学成绩,制成如下频率分布表:
某市十所重点中学进行高二联考共有5000名学生,为了了解数学学科的学习情况,现从中随机的抽取若干名学生在这次测试中的数学成绩,制成如下频率分布表:
(1)根据上面的频率分布表,推出①,②,③,④处的数字分别为3,0.025,0.1,1;
(2)在所给的坐标系中画出[80,150]上的频率分布直方图;
(3)根据题中的信息估计总体120分及以上的学生人数为2550人;
(4)在抽取的样本中,在抽取2人,求这两人分数恰好都在[100,110)的概率.
 某市十所重点中学进行高二联考共有5000名学生,为了了解数学学科的学习情况,现从中随机的抽取若干名学生在这次测试中的数学成绩,制成如下频率分布表:
某市十所重点中学进行高二联考共有5000名学生,为了了解数学学科的学习情况,现从中随机的抽取若干名学生在这次测试中的数学成绩,制成如下频率分布表:| 分组 | 频数 | 频率 |
| [80,90) | ① | ② |
| [90,100) | 0.050 | |
| [100,110) | 0.200 | |
| [110,120) | 36 | 0.300 |
| [120,130) | 0.275 | |
| [130,140) | 12 | ③ |
| [140,150] | 0.050 | |
| 合计 | ④ |
(2)在所给的坐标系中画出[80,150]上的频率分布直方图;
(3)根据题中的信息估计总体120分及以上的学生人数为2550人;
(4)在抽取的样本中,在抽取2人,求这两人分数恰好都在[100,110)的概率.
6.函数f(x)=x3+sinx+2(x∈R),若f(a)=2,则f(-a)的值为( )
| A. | 5 | B. | -2 | C. | 1 | D. | 2 |
20.若直线x=-1的倾斜角为α,则α=( )
| A. | 0° | B. | 45° | C. | 90° | D. | 不存在 |
4.下列函数中,是偶函数且不存在零点的是( )
| A. | y=x2 | B. | y=$\sqrt{x}$ | C. | y=log2x | D. | y=($\frac{1}{2}$)|x| |
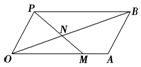 如图所示,四边形OABP是平行四边形,过点P的直线与射线OA,OB分别相交于点M,N,若$\overrightarrow{OM}$=x$\overrightarrow{OA}$,$\overrightarrow{ON}$=y$\overrightarrow{OB}$.
如图所示,四边形OABP是平行四边形,过点P的直线与射线OA,OB分别相交于点M,N,若$\overrightarrow{OM}$=x$\overrightarrow{OA}$,$\overrightarrow{ON}$=y$\overrightarrow{OB}$.