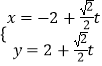Question

【题目】设函数 ，其中 ,若存在唯一的整数 ，使得 ，则 的取值范围是（ ）
A.
B.
C.
D.

Answer 1

【答案】A
【解析】设 . 恒过( ， 恒过(1,0)
因为存在唯一的整数 ，使得 ，所以存在唯一的整数 ，使得 在直线 下方.
因为 ，
所以当 时， , 单调递减；
当 时， , 单调递增.
所以 .作出函数图象如图所示：

根据题意得： ，解得： .
故答案为：A.
根据题目中所给的条件的特点，先构造函数g（x）=ex（2x-1），h（x）=mx-m，将原问题转化为：存在唯一的整数x0使得g（x0）在直线y=mx-m的下方.最后利用导数知识求函数的极值，结合图形可得关于字母m的不等关系，解关于m的不等式组可得m 的取值范围．