题目内容
【题目】已知曲线 ![]() 的参数方程为
的参数方程为 ![]() (
( ![]() 为参数),直线
为参数),直线 ![]() 的参数方程为
的参数方程为 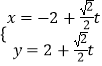 (
( ![]() 为参数).
为参数).
(Ⅰ)求曲线 ![]() 和直线
和直线 ![]() 的普通方程;
的普通方程;
(Ⅱ)若点 ![]() 为曲线
为曲线 ![]() 上一点,求点
上一点,求点 ![]() 到直线
到直线 ![]() 的距离的最大值.
的距离的最大值.
【答案】解:(Ⅰ)消去参数 ![]() 可得曲线
可得曲线 ![]() 的普通方程
的普通方程 ![]() ,
,
消去参数 ![]() 可得直线
可得直线 ![]() 的普通方程为
的普通方程为 ![]() ;
;
(Ⅱ)∵点 ![]() 为曲线
为曲线 ![]() 上一点,
上一点,
∴点 ![]() 的坐标为
的坐标为 ![]() ,
,
根据点到直线的距离公式,得![]() .
.
∴ ![]()
【解析】(1)利用cos2θ+sin2θ=1可得曲线C的直角坐标方程.消去参数t可得:直线l的直角坐标方程.
(2)设P(2cosθ,sinθ),直线l为 x y + 4 = 0 ,利用点到直线的距离公式、三角函数的单调性即可得出.
【考点精析】本题主要考查了椭圆的参数方程的相关知识点,需要掌握椭圆![]()
![]() 的参数方程可表示为
的参数方程可表示为![]() 才能正确解答此题.
才能正确解答此题.

练习册系列答案
相关题目