题目内容
(本小题满分12分)椭圆的两个焦点分别为F1(0,-2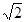 ),F2(0,2
),F2(0,2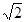 ),离心率e =
),离心率e =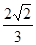 。(Ⅰ)求椭圆方程;(Ⅱ)一条不与坐标轴平行的直线l与椭圆交于不同的两点M、N,且线段MN中点的横坐标为-
。(Ⅰ)求椭圆方程;(Ⅱ)一条不与坐标轴平行的直线l与椭圆交于不同的两点M、N,且线段MN中点的横坐标为-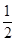 ,求直线l倾斜角的取值范围。
,求直线l倾斜角的取值范围。
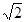 ),F2(0,2
),F2(0,2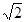 ),离心率e =
),离心率e =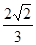 。(Ⅰ)求椭圆方程;(Ⅱ)一条不与坐标轴平行的直线l与椭圆交于不同的两点M、N,且线段MN中点的横坐标为-
。(Ⅰ)求椭圆方程;(Ⅱ)一条不与坐标轴平行的直线l与椭圆交于不同的两点M、N,且线段MN中点的横坐标为-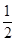 ,求直线l倾斜角的取值范围。
,求直线l倾斜角的取值范围。解 (Ⅰ)设椭圆方程为 +
+ =1。由已知,c=2
=1。由已知,c=2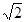 ,由e=
,由e=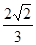 解得a=3,∴b=1。∴
解得a=3,∴b=1。∴ +x2=1为所求椭圆方程。
+x2=1为所求椭圆方程。
(Ⅱ)设直线l的方程为y=kx+b(k≠0)
解方程组
将①代入②并化简,得(k2+9)x2+2kbx+b2-9=0。
∴ 。 由于k≠0
。 由于k≠0
则化简后,得
将④代入③化简后,得k4+6k2-27>0
解得k2>3, ∴k< - 或k>
或k>
由已知,倾斜角不等于 ,
,
∴l倾斜角的取值范围是( ,
, )∪(
)∪( ,
, )。
)。
 +
+ =1。由已知,c=2
=1。由已知,c=2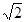 ,由e=
,由e=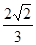 解得a=3,∴b=1。∴
解得a=3,∴b=1。∴ +x2=1为所求椭圆方程。
+x2=1为所求椭圆方程。(Ⅱ)设直线l的方程为y=kx+b(k≠0)
解方程组

将①代入②并化简,得(k2+9)x2+2kbx+b2-9=0。
∴
 。 由于k≠0
。 由于k≠0则化简后,得

将④代入③化简后,得k4+6k2-27>0
解得k2>3, ∴k< -
 或k>
或k>
由已知,倾斜角不等于
 ,
,∴l倾斜角的取值范围是(
 ,
, )∪(
)∪( ,
, )。
)。略

练习册系列答案
相关题目
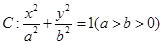 的离心率为
的离心率为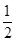 ,直线
,直线 过点
过点 ,
,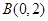 ,且与椭圆
,且与椭圆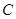 相切于点
相切于点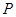 .
.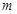 与椭圆
与椭圆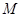 、
、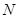 ,使得
,使得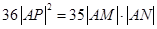 ?若存在,试求出直线
?若存在,试求出直线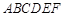 的两个顶点
的两个顶点 为椭圆的两个焦点,其余四个顶点在
为椭圆的两个焦点,其余四个顶点在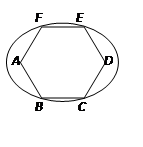
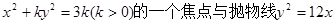 的焦点重合,则该椭圆的离心率是( )
的焦点重合,则该椭圆的离心率是( )

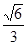
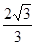
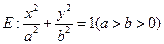 的离心率为
的离心率为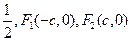 分别是左、右焦点,过F1的直线与圆
分别是左、右焦点,过F1的直线与圆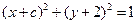 相切,且与椭圆E交于A、B两点。
相切,且与椭圆E交于A、B两点。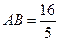 时,求椭圆E的方程;
时,求椭圆E的方程;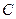 的焦点分别为
的焦点分别为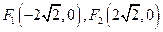 ,且过点
,且过点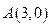 .
.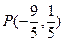 为椭圆
为椭圆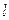 交椭圆
交椭圆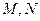 两点,且
两点,且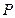 为线段
为线段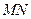 的中点,求直线
的中点,求直线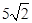 )和(0,-
)和(0,-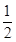 ,求此椭圆方程.
,求此椭圆方程.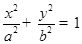 (a>b>0)的离心率为
(a>b>0)的离心率为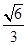 ,短轴一个端点到右焦点的距离为
,短轴一个端点到右焦点的距离为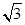
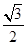 ,求△AOB面积的最大值.
,求△AOB面积的最大值.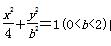 的离心率等于
的离心率等于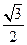 ,抛物线C2:x2=2py(p>0)的焦点在椭圆C1的顶点上.
,抛物线C2:x2=2py(p>0)的焦点在椭圆C1的顶点上.