题目内容
(本题满分14分)
已知椭圆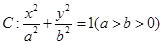 的离心率为
的离心率为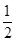 ,直线
,直线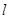 过点
过点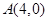 ,
,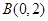 ,且与椭圆
,且与椭圆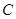 相切于点
相切于点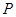 .
.
(Ⅰ)求椭圆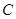 的方程;
的方程;
(Ⅱ)是否存在过点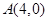 的直线
的直线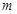 与椭圆
与椭圆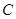 相交于不同的两点
相交于不同的两点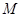 、
、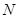 ,使得
,使得
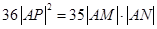 ?若存在,试求出直线
?若存在,试求出直线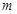 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
已知椭圆
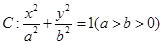 的离心率为
的离心率为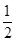 ,直线
,直线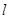 过点
过点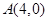 ,
,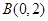 ,且与椭圆
,且与椭圆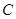 相切于点
相切于点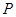 .
.(Ⅰ)求椭圆
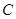 的方程;
的方程;(Ⅱ)是否存在过点
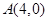 的直线
的直线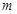 与椭圆
与椭圆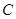 相交于不同的两点
相交于不同的两点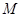 、
、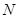 ,使得
,使得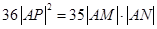 ?若存在,试求出直线
?若存在,试求出直线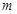 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.解: (Ⅰ)由题得过两点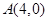 ,
,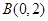 直线
直线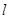 的方程为
的方程为 .………… 1分
.………… 1分
因为 ,所以
,所以 ,
, .
.
设椭圆方程为 ,
,
由 消去
消去 得,
得, .
.
又因为直线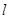 与椭圆
与椭圆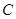 相切,所以
相切,所以 ,解得
,解得 .
.
所以椭圆方程为 . ……………………………………………… 5分
. ……………………………………………… 5分
(Ⅱ)易知直线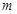 的斜率存在,设直线
的斜率存在,设直线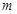 的方程为
的方程为 ,…………………… 6分
,…………………… 6分
由 消去
消去 ,整理得
,整理得 . ………… 7分
. ………… 7分
由题意知 ,
,
解得 . ……………………………………………………………… 8分
. ……………………………………………………………… 8分
设 ,
, ,则
,则 ,
, . …… 9分
. …… 9分
又直线 与椭圆
与椭圆 相切,
相切,
由 解得
解得 ,所以
,所以 . ……………………………10分
. ……………………………10分
则 . 所以
. 所以 .
.
又





所以 ,解得
,解得 .经检验成立. …………………… 13分
.经检验成立. …………………… 13分
所以直线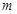 的方程为
的方程为 . …………………………………… 14分
. …………………………………… 14分
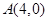 ,
,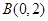 直线
直线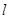 的方程为
的方程为 .………… 1分
.………… 1分因为
 ,所以
,所以 ,
, .
. 设椭圆方程为
 ,
,由
 消去
消去 得,
得, .
.又因为直线
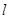 与椭圆
与椭圆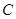 相切,所以
相切,所以 ,解得
,解得 .
.所以椭圆方程为
 . ……………………………………………… 5分
. ……………………………………………… 5分(Ⅱ)易知直线
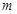 的斜率存在,设直线
的斜率存在,设直线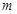 的方程为
的方程为 ,…………………… 6分
,…………………… 6分由
 消去
消去 ,整理得
,整理得 . ………… 7分
. ………… 7分由题意知
 ,
,解得
 . ……………………………………………………………… 8分
. ……………………………………………………………… 8分设
 ,
, ,则
,则 ,
, . …… 9分
. …… 9分又直线
 与椭圆
与椭圆 相切,
相切,由
 解得
解得 ,所以
,所以 . ……………………………10分
. ……………………………10分则
 . 所以
. 所以 .
.又






所以
 ,解得
,解得 .经检验成立. …………………… 13分
.经检验成立. …………………… 13分所以直线
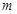 的方程为
的方程为 . …………………………………… 14分
. …………………………………… 14分略

练习册系列答案
相关题目
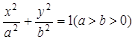 上的一个动点,且P与椭圆长轴两个顶点连线的斜率之积为
上的一个动点,且P与椭圆长轴两个顶点连线的斜率之积为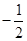 ,则椭圆的离心率为( )
,则椭圆的离心率为( )
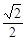
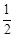
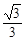
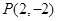 且与
且与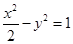 有相同渐近线的双曲线方程是
有相同渐近线的双曲线方程是



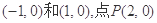 在椭圆上,则椭圆的方程为( )
在椭圆上,则椭圆的方程为( )



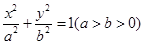 的一个焦点和一个顶点得到的直线方程为
的一个焦点和一个顶点得到的直线方程为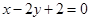 ,则该椭圆的离心率为( )
,则该椭圆的离心率为( )



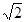 ),F2(0,2
),F2(0,2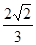 。(Ⅰ)求椭圆方程;(Ⅱ)一条不与坐标轴平行的直线l与椭圆交于不同的两点M、N,且线段MN中点的横坐标为-
。(Ⅰ)求椭圆方程;(Ⅱ)一条不与坐标轴平行的直线l与椭圆交于不同的两点M、N,且线段MN中点的横坐标为-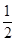 ,求直线l倾斜角的取值范围。
,求直线l倾斜角的取值范围。 ,过椭圆的右焦点且与x轴垂直的直线与椭圆交于P、Q两点,椭圆的右准线与x轴交于点M,若
,过椭圆的右焦点且与x轴垂直的直线与椭圆交于P、Q两点,椭圆的右准线与x轴交于点M,若 为正三角形,则椭圆的离心率等于 ▲
为正三角形,则椭圆的离心率等于 ▲ 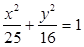 的长轴
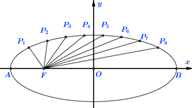
的长轴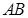 分成
分成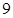 等分,过每个分点作
等分,过每个分点作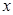 轴的垂线交椭圆的上半部分于
轴的垂线交椭圆的上半部分于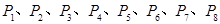 八个点,
八个点,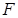 是椭圆的左焦点,则
是椭圆的左焦点,则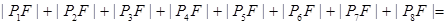 .
.
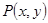 是椭圆
是椭圆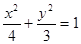 上的动点,
上的动点,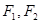 为其左、右焦点,则
为其左、右焦点,则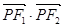 的取值范围是 ▲ 。
的取值范围是 ▲ 。