题目内容

19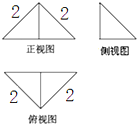．把边长为2的正方形ABCD沿对角线BD折起，形成的三棱锥A-BCD的三视图如图所示，则这个三棱锥的表面积为（　　）
A．2$\sqrt{3}$+4B．4$\sqrt{3}$C．8D．2$\sqrt{3}$+2

分析 结合直观图，根据正视图、俯视图均为全等的等腰直角三角形，可得平面BCD⊥平面ABD，分别求得△BDC和△ABD的高，即为侧视图直角三角形的两直角边长，代入面积公式计算．

解答 解：如图：∵正视图、俯视图均为全等的等腰直角三角形，
∴平面BCD⊥平面ABD，
又O为BD的中点，∴CO⊥平面ABD，OA⊥平面BCD，
三角形ACD与△ABC均为等边三角形，边长为2，所以面积相等为$\sqrt{3}$，
又△ABD和△BCD面积和为正方形的面积4，
∴三棱锥C-ABD的表面积为2$\sqrt{3}$+4．
故选A．

点评 本题考查了由正视图、俯视图求几何体的表面积，判断几何体的特征及相关几何量的数据是关键．

练习册系列答案
相关题目
12．在△ABC中，|AB|=1，|AC|=$\sqrt{3}$，若|$\overrightarrow{AB}$+$\overrightarrow{AC}$|=|$\overrightarrow{BC}$|，则其形状为③；若?λ∈R使|λ$\overrightarrow{AB}$-$\overrightarrow{AC}$|≤$\sqrt{2}$成立，则$\overrightarrow{AB}$•$\overrightarrow{AC}$的范围是$（-\sqrt{3}，-1]∪[1，\sqrt{3}）$
（①锐角三角形 ②钝角三角形  ③直角三角形，在横线上填上序号）．
11．如图，在五棱锥P-ABCDE中，PA⊥平面ABCDE，AB∥CD，AC∥ED，AE∥BC，∠ABC=45°，AB=2$\sqrt{2}$，BC=2AE=4，三角形PAB是等腰三角形．
（1）求证：平面PCD⊥平面PAC；
（2）求直线PB与平面PCD所成角的大小．
7．清华大学自主招生考试题中要求考生从A，B，C三道题中任选一题作答，考试结束后，统计数据显示共有600名学生参加测试，选择A，B，C三题答卷数如下表：
题ABC
答卷数180300120
（Ⅰ）负责招生的教授为了解参加测试的学生答卷情况，现用分层抽样的方法从600份答案中抽出若干份答卷，其中从选择A题作答的答卷中抽出了3份，则应分别从选择B，C题作答的答卷中各抽出多少份？
（Ⅱ）测试后的统计数据显示，A题的答卷得优的有60份，若以频率作为概率，在（Ⅰ）问中被抽出的选择A题作答的答卷中，记其中得优的份数为X，求X的分布列及其数学期望E（X）．
14．在直三棱柱ABC-A1B1C1中，AB⊥AC，AA1=AC=2AB，M是CC1的中点，N是棱AC上的点，且$\overrightarrow{{A_1}N}⊥\overrightarrow{BM}，|{\overrightarrow{{A_1}N}}|=2\sqrt{5}$，求三棱锥A1-ABN的体积．
4．已知抛物线C1：y2=2x及圆C2：（x-1）2+y2=1．点P（a，b）为C1上一点．
（Ⅰ）当a=2时，求过点P的圆C2的切线方程；
（Ⅱ）当a＞2时，过点P作圆C2的两条切线l1，l2分别与y轴交于B，C两点，求△PBC的面积的最小值．
10．已知三角形ABC三边长分别为x、y、1且x，y∈（0，1），则△ABC为锐角三角形的概率是2-$\frac{π}{2}$．
6．已知函数f（x）=$\frac{{{{（2x-m）}^2}}}{2-x}$x∈（0，1]，它的一个极值点是x=$\frac{1}{2}$
（Ⅰ）求m的值及f（x）在x∈（0，1]上的值域；
（Ⅱ）设函数 g（x）=ex+$\sqrt{x}$-2x，求证：函数y=f（x）与y=g（x）的图象在x∈（0，1]上没有公共点．
6．已知三棱锥的三视图如图所示，其中正视图是正三角形，侧视图是直角三角形，则该三棱锥的体积是（　　）
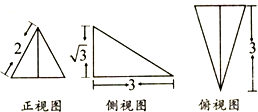
A．2B．$\frac{2\sqrt{3}}{3}$C．3$\sqrt{3}$D．$\sqrt{3}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网