题目内容
已知椭圆 :
: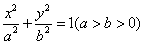 ,右焦点
,右焦点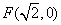 ,点
,点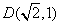 在椭圆上.
在椭圆上.
(I)求椭圆 的标准方程;
的标准方程;
(II) 已知直线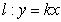 与椭圆
与椭圆 交于
交于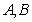 两点,
两点,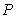 为椭圆
为椭圆 上异于
上异于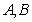 的动点.
的动点.
(i)若直线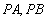 的斜率都存在,证明:
的斜率都存在,证明: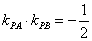 ;
;
(ii) 若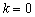 ,直线
,直线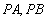 分别与直线
分别与直线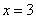 相交于点
相交于点 ,直线
,直线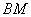 与椭圆
与椭圆 相交
相交
于点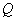 (异于点
(异于点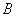 ), 求证:
), 求证: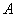 ,
,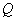 ,
,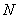 三点共线.
三点共线.
解:(Ⅰ)依题意,椭圆的焦点为 ,则
,则 ,
,
解得 ,所以
,所以 .
.
故椭圆 的标准方程为
的标准方程为 . ……………5分
. ……………5分
(Ⅱ)(i)证明:设 ,则
,则

两式作差得 .
.
因为直线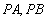 的斜率都存在,所以
的斜率都存在,所以 .
.
所以  ,即
,即 .
.
所以,当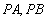 的斜率都存在时,
的斜率都存在时,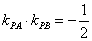 . ……………9分
. ……………9分
(ii) 证明: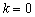 时,
时,  .
.
设 的斜率为
的斜率为 ,则
,则 的斜率为
的斜率为 ,
,
直线 ,
, ,
,
直线 ,
,  ,
,
所以直线 ,直线
,直线 ,
,
联立,可得交点 .
.
因为 ,
,
所以点 在椭圆
在椭圆 上.
上.
即直线 与直线
与直线 的交点
的交点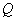 在椭圆上,即
在椭圆上,即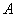 ,
,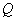 ,
,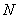 三点共线. ……………14分
三点共线. ……………14分

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
 的值域为______________
的值域为______________ (
( R)是奇函数,其部分图象如图所示,则在
R)是奇函数,其部分图象如图所示,则在 上与函数
上与函数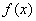 的单调性相同的是
的单调性相同的是 B.
B.  C.
C.  D.
D. 

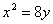 被直线
被直线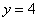 分成两个区域
分成两个区域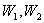 (包括边界),
(包括边界),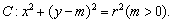
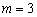 ,则圆心C到抛物线上任意一点距离的最小值是__________;
,则圆心C到抛物线上任意一点距离的最小值是__________; 内(包括边界)且与三侧边界均有公共点,则圆C的半径是__________.
内(包括边界)且与三侧边界均有公共点,则圆C的半径是__________.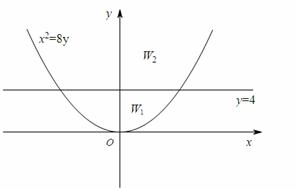
 外接圆的圆心为O,AB=2,AC=3,BC=
外接圆的圆心为O,AB=2,AC=3,BC= ,则
,则 ·
· =________.
=________.
 求tan θ的值;
求tan θ的值; 1,-2),b=(1+m,1-m),若a∥b,则实数m的值为________.
1,-2),b=(1+m,1-m),若a∥b,则实数m的值为________. sin C,B=30°,那么角A=________.
sin C,B=30°,那么角A=________.