题目内容
已知![]() 矩形ABCD所在平面,PA=AD=
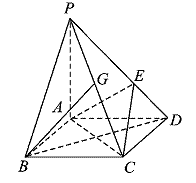
矩形ABCD所在平面,PA=AD=![]() ,E为线段PD上一点,G为线段PC的中点。
,E为线段PD上一点,G为线段PC的中点。
(1)当E为PD的中点时,求证:![]()
(2)当![]() 时,求证:BG//平面AEC。
时,求证:BG//平面AEC。
 |
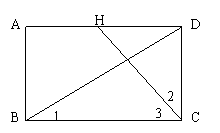
(1)过E作EH⊥AD,垂足为H,连接CH。
 |
![]() ,
,![]() ,
,
∴![]()
又![]() ,∴
,∴![]() ,∴BD⊥CH,
,∴BD⊥CH,
∴BD⊥CE。 (6分)
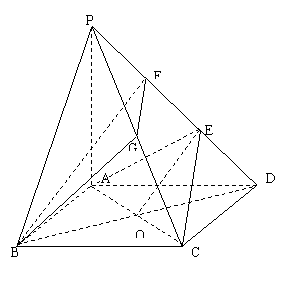
(2)取PE的中点F,连接GF,BF。
 |
∵G为PC的中点,
∴GF//CE
∴GF//平面ACE。连接BD交AC与点O,连接OE.
∵E为DF的中点,
∴BF//OE
∴BF//平面ACE。∵![]() ,
,
∴平面BGF//平面AEC。
又![]() ∴BG//平面AEC。 (12分)
∴BG//平面AEC。 (12分)
(该题还可以建立空间直角坐标系来解答。)

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
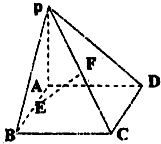 如图,已知矩形ABCD所在平面外一点P,PA⊥平面ABCD,E、F分别是AB、PC的中点,
如图,已知矩形ABCD所在平面外一点P,PA⊥平面ABCD,E、F分别是AB、PC的中点,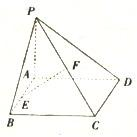 10、如图,已知矩形ABCD所在平面外一点P,PA⊥平面ABCD,E、F分别是AB,PC的中点.
10、如图,已知矩形ABCD所在平面外一点P,PA⊥平面ABCD,E、F分别是AB,PC的中点. 如图,已知矩形ABCD所在平面外一点P,PA⊥平面ABCD,E、F分别是AB、PC的中点.
如图,已知矩形ABCD所在平面外一点P,PA⊥平面ABCD,E、F分别是AB、PC的中点.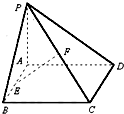 如图,已知矩形ABCD所在平面外一点P,PA⊥平面ABCD,AB=1,BC=2,PA=2,E、F分别是AB、PC的中点.
如图,已知矩形ABCD所在平面外一点P,PA⊥平面ABCD,AB=1,BC=2,PA=2,E、F分别是AB、PC的中点.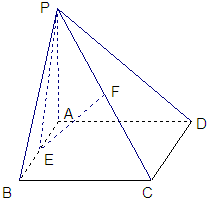 如图,已知矩形ABCD所在平面外一点P,PA⊥平面ABCD,AB=2,∠PDA=45°,E、F分别是AB、PC的中点.
如图,已知矩形ABCD所在平面外一点P,PA⊥平面ABCD,AB=2,∠PDA=45°,E、F分别是AB、PC的中点.