Question

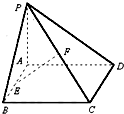如图，已知矩形ABCD所在平面外一点P，PA⊥平面ABCD，AB=1，BC=2，PA=2，E、F分别是AB、PC的中点．
（1）求证：EF∥平面PAD；
（2）求证：CD⊥EF
（3）求EF与平面ABCD所成的角的大小．

Answer 1

分析：（1）建立空间直角坐标系，用坐标表示向量，确定

EF

与

AP

，

AD

共面，即可证明EF∥平面PAD；
（2）证明

CD

•

EF

=0，即可得到结论；
（3）利用向量的夹角公式，计算＜

EF

，

AP

＞=45°，从而可求EF与平面ABCD所成的角的大小．

解答：（1）证明：如图，建立空间直角坐标系A-xyz，则：A（0，0，0），B（1，0，0），C（1，2，0），D（0，2，0），P（0，0，2）
∵E为AB的中点，F为PC的中点，
∴E（

1

2

，0，0），F（

1

2

，1，1）
∴

EF

=(0，1，1)，

AP

=(0，0，2)，

AD

=(0，2，0)
∴

EF

=

1

2

(

AP

+

AD

)
∴

EF

与

AP

，

AD

共面
∵E∉平面PAD，
∴EF∥平面PAD；
（2）证明：∵

CD

=(-1，0，0)
∴

CD

•

EF

=（-1，0，0）•（0，1，1）=0
∴CD⊥EF；
（3）解：∵

EF

=(0，1，1)，

AP

=(0，0，2)
∴cos＜

EF

，

AP

＞=

EF • AP

| EF || AP |

=

2

2 •2

=

2

2

∴＜

EF

，

AP

＞=45°
∵

AP

⊥平面AC
∴

AP

是平面AC的法向量
∴EF与平面AC所成的角为90°-＜

EF

，

AP

＞=45°．

点评：本题考查线面平行，考查线线垂直，考查线面角，考查向量知识的运用，考查学生分析解决问题的能力，属于中档题．