题目内容
20.已知f(x)是定义在R上的奇函数,满足f(x)+f(2-x)=0,且当x∈[0,1)时,f(x)=ln(ex+$\frac{x}{x+1}$),则函数g(x)=f(x)+$\frac{1}{3}$x在区间[-6,6]上的零点个数是( )| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
分析 利用抽象函数求出函数的对称中心以及函数的周期,利用数形结合判断函数的交点个数,得到零点个数.
解答 解:由f(x)+f(2-x)=0,令x=1,则f(1)=0,
∵f(x)+f(2-x)=0,∴f(x)的图象关于点(1,0)对称,
又f(x)是定义在R上的奇函数,∴f(x)=-f(2-x)=f(x-2),
∴f(x)是周期为2的函数.
当x∈[0,1)时,f(x)=ln(ex+$\frac{x}{x+1}$)=ln(ex-$\frac{1}{x+1}$+1)为增函数,
画出f(x)及y=-$\frac{1}{3}x$在[0,6]上的图象如图所示,
经计算,结合图象易知,函数f(x)的图象与直线y=-$\frac{1}{3}x$,
在[0,6]上有3个不同的交点,由函数的奇偶性可知,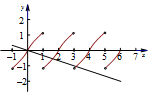
函数g(x)=f(x)+$\frac{1}{3}$x在区间[-6,6]上的零点个数是5.
故选:B.
点评 本题考查函数的零点个数的判断,抽象函数的应用,考查数形结合以及计算能力.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案
相关题目
12.甲,乙两台机床同时生产一种零件,其质量按测试指标划分:指标大于或等于100为优品,大于等于90且小于100为合格品,小于90为次品,现随机抽取这两台车床生产的零件各100件进行检测,检测结果统计如下:
(1)试分别估计甲机床、乙机床生产的零件为优品的概率;
(2)甲机床生产一件零件,若是优品可盈利160元,合格品可盈利100元,次品则亏损20元;假设甲机床某天生产50件零件,请估计甲机床该天的日利润(单位:元);
(3)从甲、乙机床生产的零件指标在[90,95)内的零件中,采用分层抽样的方法抽取5件,从这5件中任选2件进行质量分析,求这2件都是乙机床生产的概率.
| 测试指标 | [85,90) | [90,95) | [95,100) | [100,105) | [105,110) |
| 机床甲 | 8 | 12 | 40 | 32 | 8 |
| 机床乙 | 7 | 18 | 40 | 29 | 6 |
(2)甲机床生产一件零件,若是优品可盈利160元,合格品可盈利100元,次品则亏损20元;假设甲机床某天生产50件零件,请估计甲机床该天的日利润(单位:元);
(3)从甲、乙机床生产的零件指标在[90,95)内的零件中,采用分层抽样的方法抽取5件,从这5件中任选2件进行质量分析,求这2件都是乙机床生产的概率.
9.已知双曲线$M:\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的左、右焦点分别为F1、F2,|F1F2|=2c.若双曲线M的右支上存在点P,使$\frac{a}{{sin∠P{F_1}{F_2}}}=\frac{3c}{{sin∠P{F_2}{F_1}}}$,则双曲线M的离心率的取值范围为( )
| A. | $(1,\frac{{2+\sqrt{7}}}{3})$ | B. | $(1,\frac{{2+\sqrt{7}}}{3}]$ | C. | (1,2) | D. | (1,2] |
10.已知双曲线过点(2,3),渐进线方程为y=±$\sqrt{3}$x,则双曲线的标准方程是( )
| A. | $\frac{{7{x^2}}}{16}-\frac{y^2}{12}=1$ | B. | $\frac{y^2}{3}-\frac{x^2}{2}=1$ | C. | ${x^2}-\frac{y^2}{3}=1$ | D. | $\frac{{3{y^2}}}{23}-\frac{x^2}{23}=1$ |
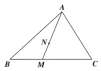 如图,在△ABC中,M为BC上不同于B,C的任意一点,点N满足$\overrightarrow{AN}=2\overrightarrow{NM}$.若$\overrightarrow{AN}=x\overrightarrow{AB}+y\overrightarrow{AC}$,则x2+9y2的最小值为$\frac{2}{5}$.
如图,在△ABC中,M为BC上不同于B,C的任意一点,点N满足$\overrightarrow{AN}=2\overrightarrow{NM}$.若$\overrightarrow{AN}=x\overrightarrow{AB}+y\overrightarrow{AC}$,则x2+9y2的最小值为$\frac{2}{5}$.