题目内容
12.甲,乙两台机床同时生产一种零件,其质量按测试指标划分:指标大于或等于100为优品,大于等于90且小于100为合格品,小于90为次品,现随机抽取这两台车床生产的零件各100件进行检测,检测结果统计如下:| 测试指标 | [85,90) | [90,95) | [95,100) | [100,105) | [105,110) |
| 机床甲 | 8 | 12 | 40 | 32 | 8 |
| 机床乙 | 7 | 18 | 40 | 29 | 6 |
(2)甲机床生产一件零件,若是优品可盈利160元,合格品可盈利100元,次品则亏损20元;假设甲机床某天生产50件零件,请估计甲机床该天的日利润(单位:元);
(3)从甲、乙机床生产的零件指标在[90,95)内的零件中,采用分层抽样的方法抽取5件,从这5件中任选2件进行质量分析,求这2件都是乙机床生产的概率.
分析 (1)先分别求出甲机床为优品的频率和乙机床为优品的频率,由此能估计甲、乙两机床为优品的概率.
(2)求出甲机床被抽产品每1件的平均数利润为,从而估计甲机床每生产1件的利润,由此能求出甲机床某天生产50件零件的利润.
(3)由题意知,甲机床应抽取2,乙机床应抽取3,记甲机床的2个零件为A,B,乙机床的3个零件为a,b,c,由此利用列举法能示出这2件都是乙机床生产的概率.
解答 解:(1)因为甲机床为优品的频率为$\frac{32+8}{100}=\frac{2}{5}$,
乙机床为优品的频率约为$\frac{29+6}{100}=\frac{7}{20}$,
所以估计甲、乙两机床为优品的概率分别为$\frac{2}{5},\frac{7}{20}$;
(2)甲机床被抽产品每1件的平均数利润为:
$\frac{1}{100}(40×160+52×100-8×20)=114.4$元
所以估计甲机床每生产1件的利润为114.4元
所以甲机床某天生产50件零件的利润为50×114.4=5720元
(3)由题意知,甲机床应抽取$5×\frac{12}{30}=2$,
乙机床应抽取$5×\frac{18}{30}=3$,
记甲机床的2个零件为A,B,乙机床的3个零件为a,b,c,
若从5件中选取2件分别为AB,Aa,Ab,Ac,Ba,Bb,Bc,ab,ac,bc共10种取法
满足条件的共有3种,分别为ab,ac,bc,
所以,这2件都是乙机床生产的概率$P=\frac{3}{10}$.
点评 本题考查古典概型及应用,考查概率的计算,考查计数原理,解题时要要认真审题,注意列举法的合理运用,是基础题.

练习册系列答案
相关题目
2.直线l与平面α有无数个公共点,那么1与α的位置关系为( )
| A. | l∥α | B. | l?α | C. | l⊥α | D. | 以上都不对 |
17.已知集合A={x∈Z|(2x+3)(x-3)<0},B={x|y=$\sqrt{1-lnx}$},则A∩B=( )
| A. | (0,e] | B. | {0,e} | C. | {1,2} | D. | (1,2) |
1.已知复数$z=\frac{1}{1+i}$,则z的虚部为( )
| A. | $\frac{1}{2}i$ | B. | $-\frac{1}{2}i$ | C. | $\frac{1}{2}$ | D. | $-\frac{1}{2}$ |
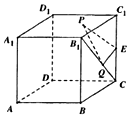 如右图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E为棱CC1的中点,点P,Q分别为面A1B1C1D1和线段B1C上的动点,则△PEQ周长的最小值为$\sqrt{10}$.
如右图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E为棱CC1的中点,点P,Q分别为面A1B1C1D1和线段B1C上的动点,则△PEQ周长的最小值为$\sqrt{10}$.