题目内容
如图,圆O1和圆O2的半径都等于1,O1O2=4,过动点P分别作圆O1、圆O2的切线PM、PN(M、N为切点),使得PM=2PN,试建立平面直角坐标系,并求动点P的轨迹方程.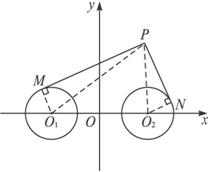
解：以O1O2的中点O为原点,O1O2所在的直线为x轴,建立如图所示的平面直角坐标系,则O1(-2,0)、O2(2,0).
由已知PM=
PN,得PM2=2PN2.
因为两圆的半径均为1,所以PO12-1=2(PO22-1).
设P(x,y),则(x+2)2+y2-1=2［(x-2)2+y2-1］,
即(x-6)2+y2=33,所以所求轨迹方程为(x-6)2+y2=33(或x2+y2-12x+3=0).
练习册系列答案
开心蛙口算题卡系列答案
相关题目
PN.试建立平面直角坐标系，并求动点P的轨迹方程__________.
PN.试建立平面直角坐标系，并求动点P的轨迹方程__________.
PN，试建立平面直角坐标系，并求动点P的轨迹方程．
