题目内容
已知函数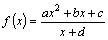 (其中
(其中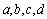 是实数常数,
是实数常数,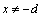 )
)
(1)若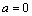 ,函数
,函数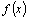 的图像关于点(—1,3)成中心对称,求
的图像关于点(—1,3)成中心对称,求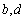 的值;
的值;
(2)若函数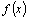 满足条件(1),且对任意
满足条件(1),且对任意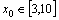 ,总有
,总有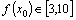 ,求
,求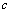 的取值范围;
的取值范围;
(3)若b=0,函数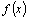 是奇函数,
是奇函数,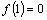 ,
,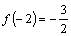 ,且对任意
,且对任意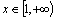 时,不等式
时,不等式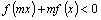 恒成立,求负实数
恒成立,求负实数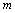 的取值范围。
的取值范围。
解(1)
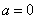 ,
,
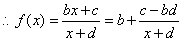 .
.
类比函数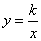 的图像,可知函数
的图像,可知函数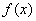 的图像的对称中心是
的图像的对称中心是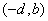 .
.
又函数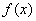 的图像的对称中心是
的图像的对称中心是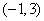 ,
,
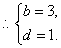
(2)由(1)知,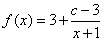 .
.
依据题意,对任意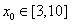 ,恒有
,恒有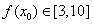 .
.
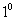 若
若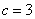 ,则
,则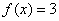 ,符
,符 合题意.
合题意.
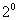 若
若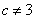 ,当
,当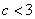 时,对任意
时,对任意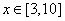 ,恒有
,恒有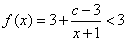 ,不符合题意.
,不符合题意.
所以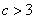 ,函数
,函数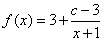 在
在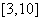 上是单调递减
上是单调递减 函数,且满足
函数,且满足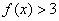 .
.
因此,当且仅当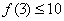 ,即
,即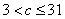 时符合题意.
时符合题意.
综上,所求实数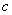 的范围是
的范围是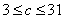 .
.
(3)依据题设,有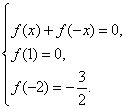 解得
解得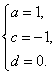
于是,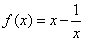 .
.
由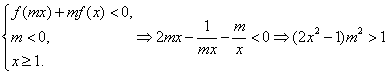 ,解得
,解得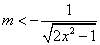 .
.
因此,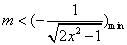 .
.
考察函数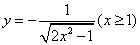 ,可知该函数在
,可知该函数在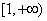 是增函数,故
是增函数,故
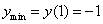 .
.
所以,所求负实数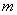 的取值范围是
的取值范围是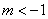 .
.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
 值是 .
值是 .
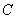 :
: ,则曲线
,则曲线 ( ).
( ).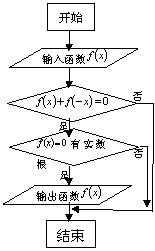


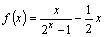
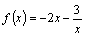
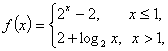 则函数
则函数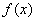 的零点为
的零点为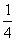 和1 B.
和1 B.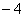 和0 C.
和0 C.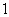
 展开式的常数项为60,则常数
展开式的常数项为60,则常数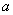 的值为 .
的值为 . n;
n;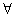 x
x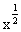 ,y=
,y=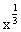 ,y=x3,其中在定义域上是增函数的有3个;
,y=x3,其中在定义域上是增函数的有3个;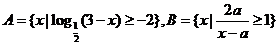 ,若
,若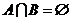 ,则实数
,则实数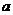 的取值范围是_______.
的取值范围是_______.