题目内容
（选做题）已知x，y为正实数，3x+2y=10，求函数W=
+
的最大值为
| 3x |
| 2y |
2
| 5 |
2
．| 5 |
分析：可以先将W平方，然后利用基本不等式的性质即可得出．
解答：解：∵x，y为正实数，3x+2y=10，
∴W2=3x+2y+2
≤10+（3x+2y）=20，当且仅当3x=2y，3x+2y=10，即x=
，y=
时取等号．
∴w≤2
．即W的最大值为2
．
故答案为2
．
∴W2=3x+2y+2
| 3x•2y |
| 5 |
| 3 |
| 5 |
| 2 |
∴w≤2
| 5 |
| 5 |
故答案为2
| 5 |
点评：熟练掌握基本不等式的性质是解题的关键．
练习册系列答案
相关题目
+
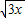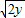的最大值为 ．