题目内容
选做题:已知x,y,z∈R+,且x+y+z=1.
(1)若2x2+3y2+6z2=1,求x,y,z的值;
(2)若2x2+3y2+tz2≥1恒成立,求正数t的取值范围.
(1)若2x2+3y2+6z2=1,求x,y,z的值;
(2)若2x2+3y2+tz2≥1恒成立,求正数t的取值范围.
分析:(1)x,y,z∈R+,且x+y+z=1,由2x2+3y2+6z2=1,令
,能求出x,y,z的值.
(2)由柯西不等式得(2x2+3y2+tz2)(
+
+
)>(x+y+z)2=1,由2x2+3y2+tz2≥1恒成立,知(
+
+
)≥1,由此能求出正数t的取值范围.
|
(2)由柯西不等式得(2x2+3y2+tz2)(
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| t |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| t |
解答:解:(1)∵x,y,z∈R+,且x+y+z=1,
∴由2x2+3y2+6z2=1,令
,
解得x=
,y=
,z=
.
(2)柯西不等式得:(2x2+3y2+tz2)(
+
+
)>(x+y+z)2=1,
∵2x2+3y2+tz2≥1恒成立,
∴(
+
+
)≥1
即
+
≥1
解得0<t≤6
∴由2x2+3y2+6z2=1,令
|
解得x=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 6 |
(2)柯西不等式得:(2x2+3y2+tz2)(
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| t |
∵2x2+3y2+tz2≥1恒成立,
∴(
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| t |
即
| 5 |
| 6 |
| 1 |
| t |
解得0<t≤6
点评:本题考查不等式的性质和应用,是基础题.解题时要认真审题,仔细解答,注意柯西不等式的灵活运用.

练习册系列答案
相关题目
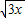 +
+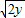 的最大值为 .
的最大值为 .