题目内容
已知函数
 ,函数
,函数
⑴当 时,求函数
时,求函数 的表达式;
的表达式;
⑵若 ,函数
,函数 在
在 上的最小值是2 ,求
上的最小值是2 ,求 的值;
的值;
(3)⑵的条件下,求直线 与函数
与函数 的图象所围成图形的面积.
的图象所围成图形的面积.
⑴当 时,函数
时,函数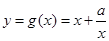
⑵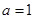
(3)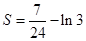
解析试题分析:(1)对x的取值分类讨论,化简绝对值,求出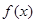 得到
得到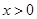 和
和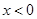 导函数相等,代入到
导函数相等,代入到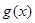 中得到即可;
中得到即可;
(2)根据基本不等式得到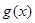 的最小值即可求出
的最小值即可求出 ;
;
(3)根据(2)知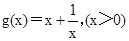 先联立直线与函数解析式求出交点,利用定积分求直线和函数图象围成面积的方法求出即可.
先联立直线与函数解析式求出交点,利用定积分求直线和函数图象围成面积的方法求出即可.
⑴∵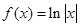 ,
,
∴当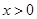 时,
时,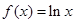 ; 当
; 当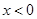 时,
时,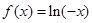
∴当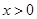 时,
时,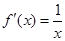 ; 当
; 当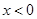 时,
时,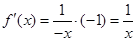 .
.
∴当 时,函数
时,函数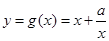 .
.
⑵∵由⑴知当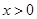 时,
时,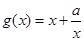 ,
,
∴当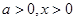 时,
时, 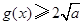 当且仅当
当且仅当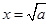 时取等号.
时取等号.
∴函数 在
在 上的最小值是
上的最小值是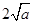 ,∴依题意得
,∴依题意得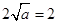 ∴
∴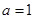 .
.
⑶由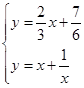 解得
解得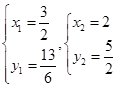
∴直线 与函数
与函数 的图象所围成图形的面积
的图象所围成图形的面积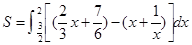 =
=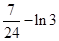
考点:利用导数研究函数的单调性,基本不等式,利用定积分求封闭图形的面积

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

 的单调区间和极值;
的单调区间和极值; ,都存在
,都存在 ,使得
,使得 ,求
,求 的取值范围
的取值范围 =
= ,试比较x0与m的大小,并加以证明.
,试比较x0与m的大小,并加以证明.
 .
. 时,求函数
时,求函数 的单调区间;
的单调区间; 时,求函数
时,求函数 上的最小值
上的最小值 和最大值
和最大值 .
. (
( R),
R), 为其导函数,且
为其导函数,且 时
时 有极小值
有极小值 .
. 的单调递减区间;
的单调递减区间; ,
, ,当
,当 时,对于任意x,
时,对于任意x, 和
和 的值至少有一个是正数,求实数m的取值范围;
的值至少有一个是正数,求实数m的取值范围; (
( 为正整数)对任意正实数
为正整数)对任意正实数 恒成立,求
恒成立,求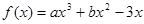 在
在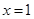 处取得极值-2.
处取得极值-2. 的解析式;
的解析式;  在点
在点 处的切线方程.
处的切线方程. 满足如下条件:当
满足如下条件:当 时,
时, ,且对任
,且对任 ,都有
,都有 .
. 处的切线方程;
处的切线方程; ,
, 时,函数
时,函数 ,
, 、
、 、
、 、
、 、
、 ,使得等式
,使得等式
 成立?若存在就求出
成立?若存在就求出 (
( ,函数
,函数 的导函数
的导函数 ,且
,且 ,其中
,其中 为自然对数的底数.
为自然对数的底数. 的极值;
的极值; ,使得不等式
,使得不等式 成立,试求实数
成立,试求实数 的取值范围;
的取值范围; .
.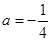 时,求函数
时,求函数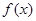 的单调区间;
的单调区间;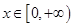 时,函数
时,函数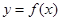 图象上的点都在
图象上的点都在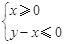 所表示的平面区域内,不等式
所表示的平面区域内,不等式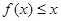 恒成立,求实数
恒成立,求实数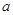 的取值范围. [来源:学科
的取值范围. [来源:学科