题目内容
已知函数
(1)求 的单调区间和极值;
的单调区间和极值;
(2)若对于任意的 ,都存在
,都存在 ,使得
,使得 ,求
,求 的取值范围
的取值范围
(1) 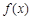 的单调增区间是
的单调增区间是 ,单调减区间是
,单调减区间是 和
和 ,当
,当 时,
时,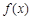 取极小值
取极小值 ,当
,当 时,
时,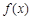 取极大值
取极大值 , (2)
, (2) 
解析试题分析:(1)求函数单调区间及极值,先明确定义域:R,再求导数 在定义域下求导函数的零点:
在定义域下求导函数的零点: 或
或 ,通过列表分析,根据导函数符号变化规律,确定单调区间及极值,即
,通过列表分析,根据导函数符号变化规律,确定单调区间及极值,即 的单调增区间是
的单调增区间是 ,单调减区间是
,单调减区间是 和
和 ,当
,当 时,
时, 取极小值
取极小值 ,当
,当 时,
时, 取极大值
取极大值 , (2)本题首先要正确转化:“对于任意的
, (2)本题首先要正确转化:“对于任意的 ,都存在
,都存在 ,使得
,使得 ”等价于两个函数值域的包含关系.设集合
”等价于两个函数值域的包含关系.设集合 ,集合
,集合 则
则 ,其次挖掘隐含条件,简化讨论情况,明确讨论方向.由于
,其次挖掘隐含条件,简化讨论情况,明确讨论方向.由于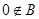 ,所以
,所以 ,因此
,因此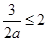 ,又
,又 ,所以
,所以 ,即
,即
解(1)由已知有 令
令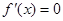 ,解得
,解得 或
或 ,列表如下:
,列表如下:






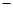



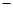



 练习册系列答案
练习册系列答案
高效课时通10分钟掌控课堂系列答案
有序启动作业精编系列答案
随堂1加1系列答案
黄冈金牌之路期末冲刺卷系列答案
勤学早期末复习系列答案
同行学案系列答案
全优点练课计划系列答案
单元双测全程提优测评卷系列答案
1课3练江苏人民出版社系列答案
 相关题目
相关题目
 为实数,
为实数,
 ;
; ,求
,求 在[-2,2] 上的最大值和最小值.
在[-2,2] 上的最大值和最小值. ,( a为常数,e为自然对数的底).
,( a为常数,e为自然对数的底).

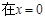 时取得极小值,试确定a的取值范围;
时取得极小值,试确定a的取值范围; 的极大值构成的函数
的极大值构成的函数 ,将a换元为x,试判断
,将a换元为x,试判断 是否能与
是否能与 (m为确定的常数)相切,并说明理由.
(m为确定的常数)相切,并说明理由. ,曲线
,曲线 在点
在点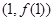 处的切线方程为
处的切线方程为


 ,其中
,其中 ,
, 为自然对数的底数。
为自然对数的底数。 是函数
是函数 的导函数,求函数
的导函数,求函数 上的最小值;
上的最小值; ,函数
,函数 内有零点,证明:
内有零点,证明: .
. .
.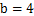 时,求
时,求 的极值;
的极值; 上单调递增,求b的取值范围.
上单调递增,求b的取值范围.
 在
在 上的最大值和最小值分别记为
上的最大值和最小值分别记为 ,求
,求 ;
; 若
若 对
对 恒成立,求
恒成立,求 的取值范围.
的取值范围. ,其中
,其中 .
. 在点
在点 处的切线方程为
处的切线方程为 ,求函数
,求函数 的解析式;
的解析式; ,不等式
,不等式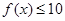 在
在 上恒成立,求
上恒成立,求 的取值范围.
的取值范围.
 ,函数
,函数
 时,求函数
时,求函数 的表达式;
的表达式; ,函数
,函数 上的最小值是2 ,求
上的最小值是2 ,求 的值;
的值; 与函数
与函数